کنترل کیفیت آماری (SPC

فهرست مطالب

بخش هفدهم؛ کنترل کیفیت آماری (Statistical Quality Control)

آنچه در این قسمت و بخش بعدی ارائه می شود تناسب بین کنترل کیفیت آماری و برنامه ریزی تولید و عملیات است. یک بینش و شهود مهم تئوری فیزیک کارخانه این است که تغییرات و نوسانات (Variability) نقش محوری در تعیین عملکرد یک سیستم تولیدی ایفا می کند. این نوسانات می‌تواند از منابع مختلفی ناشی شود از جمله خرابی ماشین، زمان تنظیم ماشین آلات، عملکرد اپراتور، تغییر در ترکیب محصول و موارد دیگر.

یکی از منابع مهم نوسان که می تواند عملکرد یک سیستم را به شدت تغییر دهد، کیفیت است. مشکلات کیفیت تقریباً همیشه به مشکل نوسانات تبدیل می شوند. به همین ترتیب، کاهش نوسانات در فرآیندها اغلب وسیله ای برای بهبود کیفیت است. از آنجایی که کیفیت و تغییرات ارتباط نزدیکی با هم دارند، ادامه مطالب را با مروری بر این موضوع مهم دنبال خواهیم کرد.

دوره های گذشته در کیفیت (The Decade of Quality)

دهه ۱۹۸۰ دهه کیفیت در آمریکا بود. تعداد زیادی کتاب در این زمینه منتشر شد، هزاران کارمند دوره‌های کوتاه مدت و سایر برنامه‌های آموزشی را گذراندند و گفتمان کیفیت (Quality Speak) به زبان رایج و استاندارد شرکت‌های آمریکایی تبدیل شد.

در سال ۱۹۸۷، سازمان بین المللی استاندارد (ISO)، سری استانداردهای کیفیت ISO 9000 را معرفی نمود. در همان سال، جایزه ملی کیفیت مالکوم بالدریج (Malcolm Baldrige National Quality Award) توسط کنگره ایالات متحده ایجاد شد.

مفهوم کیفیت، کنترل، تضمین (Assurance) و مدیریت آن در دهه ۱۹۸۰ واژه های جدیدی نبودند. کنترل کیفیت به عنوان یک رشته مطالعاتی به سال ۱۹۲۴ باز می گردد، زمانی که شوهارت (Walter A. Shewhart) از آزمایشگاه های تلفن بل وسترن الکتریک برای اولین بار نمودارهای کنترل فرآیند را معرفی کرد و اولین مقاله مهم در مورد کیفیت را در سال ۱۹۳۱ منتشر کرد.

آرماند فایگنبام (Armand Feigenbaum) اصطلاح کنترل کیفیت جامع (Total Quality Control) را در مقاله ای در سال ۱۹۵۶ ابداع کرد و از این عنوان برای نسخه جدید کتاب خود در سال ۱۹۶۱ استفاده کرد. نسخه اولیه این کتاب با عنوان کنترل کیفیت در سال ۱۹۵۱ چاپ شده بود.

در حالی که مفاهیم و ابزارهای کیفیت از خیلی قبل تر وجود داشته است اما دهه ۱۹۸۰ بود که صنعت آمریکا واقعاً به پتانسیل استراتژیک کیفیت توجه کرد. بدون شک، این علاقه تا حد زیادی با افزایش چشمگیر کیفیت محصولات ژاپنی به ویژه کاهش موجودی توسط رویکرد موفق JIT در طول دهه‌های ۱۹۷۰ و ۱۹۸۰ تحریک شده بود.

بررسی شاخص رضایت مشتری در آمریکا (American Customer Satisfaction Index -ACSI) به عنوان یک معیار مهم از رضایت مشتری که به صورت فصلی منتشر و بررسی می‌شود این نتیجه را بیان می کند که راضی کردن مشتریان دشوار تر شده است و می‌توان انتظار داشت که کیفیت یک چالش مهم برای آینده باقی بماند.

وضعیت امروز کیفیت (The Status of Quality)

تقریباً همه افراد تجربه خرید محصول بی کیفیت را داشته اند اما افراد کمی هستند که با خرید محصولی، از کیفیت فراتر از آنچه که انتظار آنرا داشته اند، ذوق زده باشند. برای مثال در صنعت خودرو (بین المللی) از روزگاری که نقض در ساخت بدنه و موتور ماشین به عنوان عیب محسوب می شده است رسیده ایم به اینکه داشتن چند پیکسل سوخته در صفحه ناوبری خودرو، عیب در نظر گرفته می شود. واضح است که کیفیت مشکلی نیست که بتوان آن را حل کرد. بهترین چیزی که می توان به آن امیدوار بود این است که با آن همگام شویم.

در حال حاضر ادبیات کیفیت را می توان به دو گروه اصلی تقسیم کرد، مدیریت کیفیت جامع (Total Quality Management -TQM) که بیشتر بر مباحث مدیریتی و ایجاد یک محیط مطلوب و حمایت کننده از بهبود کیفیت تمرکز دارد و کنترل کیفیت آماری (Statistical Quality Control -SQC) که بر کیفیت در شرایط کمی و مهندسی متمرکز است. به عنوان مثال، اندازه گیری و اطمینان از انطباق با مشخصات فنی محصول.

هر دو دیدگاه برای تدوین یک برنامه بهبود کیفیت موثر مورد نیاز است. مباحث TQM بدون SQC صرفاً کلی گویی و صحبت بدون اعداد و ارقام است، همچنین تکیه بر SQC بدون TQM تولید یکسری اعداد بدون داشتن اهدف کلی است.

تعاریف کیفیت (General Definitions)

کیفیت چیست؟ اگر بخواهیم از اندازه گیری و بهبود کیفیت صحبت کنیم، باید حداقل یک تعریف کاربردی داشته باشیم. گاروین (۱۹۸۸) پنج تعریف از کیفیت ارائه می دهد که ما آنها را به شرح زیر خلاصه می کنیم:

۱- کیفیت مترادف تعالی (Transcendent/ Excellence) است. دیدگاه مورد نظر در عبارت « نمی‌توانم کیفیت را تعریف کنم، اما وقتی می‌بینم آن را درک می کنم» خلاصه می‌شود.

۲- مبتنی بر محصول است (Product-based). کیفیت تابعی از ویژگی های محصول است برای مثال در فرش (ماشینی و دستباف) هرچه تعداد شانه و گره بالاتر باشد نشان از تراکم بهتر و کیفیت بالاتر محصول است. اینجا با خصوصیات قابل اندازه گیری سر وکار داریم. هر چه شاخص مورد نظر بیشتر، کیفیت بالاتر خواهد بود.

۳- مبتنی بر دیدگاه مصرف کننده است (User-based). کیفیت با میزان رضایت مشتری تعیین می شود. بنابراین تابعی است از هر چیزی که مشتری برایش ارزش قائل است (ویژگی های خاص، دوام، جذابیت های ظاهری و زیبایی محصول و غیره). مطابق این دیدگاه کیفیت یعنی زیبایی در چشم بیننده.

۴- مبتنی بر تولید و مراحل ساخت (Manufacturing-based). طبق این تعریف کیفیت یعنی انطباق با مشخصات فنی. به عنوان مثال آیا محصول در محدوده ابعاد تعریف شده قرار دارد. آیا به استانداردهای عملکرد اعلام شده دست یافته است. از آنجایی که این تعریف از کیفیت به طور مستقیم به فرآیندهای تولید محصولات اشاره دارد، ارتباط نزدیکی با این دیدگاه کیفیت که همان دفعه اول کار را درست و مسئولانه انجام بدهید (do it right the first time) دارد.

۵- مبتنی بر ارزش خلق شده برای مشتری است (Value-based). کیفیت به طور مشترک توسط عملکرد و قیمت تعیین می شود یعنی با قیمت مناسب، کار مصرف کننده نهایی هم راه افتاده است. اینجا دیدگاه مقرون به صرفه بودن کیفیت (Affordable Excellence) مطرح است.

این فهرست از تعاریف کیفیت دو نکته را مشخص می کند. اول، کیفیت یک مفهوم چندوجهی (Multifaceted Concept) است که فقط در شاخص های کمی و عددی خلاصه نمی شود بنابراین به چارچوبی نیاز داریم که در آن سیاست‌های کیفیت را ارزیابی کنیم.

دوم، با اینکه در تعاریف ارائه شده محصول محور بودن (Product-Oriented) وزن بیشتری دارد اما سوال این است که تعریف کیفیت باید از دیدگاه مشتری (Customer-Driven) باشد یا محصول محور؟ از آنجایی که چیزی که مشتری می بیند محصول است، کیفیت باید بر اساس محصول سنجیده شود.

اگرچه کیفیت محصول توسط مشتری مشاهده و درک می شود اما در نهایت توسط تعدادی از عوامل فرآیندی از جمله طراحی محصول، کنترل عملیات تولید و نظارت بر فرآیندها، مشارکت نیروی کار، فروش و خدمات پس از فروش و غیره تعیین می گردد.

کیفیت داخلی و خارجی (Internal versus External Quality)

برای درک بهتر رابطه بین کیفیت محصول محور و فرآیندمحور، تشخیص و تمایز بین کیفیت داخلی و خارجی مفید است :

الف) کیفیت داخلی به انطباق با مشخصات کیفی در طی مراحل تولید اشاره دارد و تقریباً معادل تعریف کیفیت مبتنی بر تولید است. کیفیت از طریق کنترل مستقیم فرآیند تولید مانند نرخ ضایعات و دوباره کاری و اقدامات غیرمستقیم شامل تغییر پارامترهای تولید به عنوان مثال تغییر فشار (در دستگاه تزریق پلاستیک) و دما (در حمام های آبکاری) نظارت می شود.

ب) کیفیت خارجی اشاره به این دارد که مشتری محصول ما را چگونه می بیند. برخی از تعاریف بالا در همین گروه جای دارند از جمله کیفیت مبتنی بر ارزش خلق شده. کیفیت خارجی را می‌توان از طریق شاخص های مستقیم رضایت مشتری مانند نرخ بازگشت محصولات، و معیارهای غیرمستقیم که از نمونه‌برداری، بازرسی، داده‌های واحد خدمات پس از فروش، نظرسنجی‌ و غیره به دست می‌آید، پایش کرد.

برای دستیابی به کیفیت خارجی بالا، باید نگرانی (نظرات) مشتری را به معیارها و کنترل هایی برای کیفیت داخلی تبدیل کرد. بنابراین، پیوند بین کیفیت داخلی و خارجی کلید توسعه یک برنامه کیفیت موثر است. موارد زیر برخی از مهم‌ترین راه‌هایی است که کیفیت داخل کارخانه را با کیفیتی که منجر به رضایت مشتری می‌شود مرتبط می کند.

۱- پیشگیری از خطا (Error prevention)؛ اگر خطاهای کمتری در حین تولید ایجاد شود، احتمال دارد عیوب کمتری در حین بازرسی از چشم ناظر پنهان و به دست مشتری برسد. تا جایی که بشود باید کیفیت را در محل تولید ارتقاء داد.

۲- بهبود بازرسی (Inspection improvement)؛ طبیعی است که اگر کارها درست انجام شود و عیوب کمتری در فرآیند تولید داشته باشیم، فشار کاری (هم ذهنی و هم جسمی) پرسنل کنترل کیفی کمتر شده و خروجی مطلوب تری را شاهد خواهیم بود. بنابراین پیشگیری و تشخیص خطا هر دو با گذشت زمان بهبود می یابند.

۳- بهبود محیط عملکرد (Environment enhancement)؛ برخی از مشکلات کیفی در کارخانه و در حین تولید قابل شناسایی نیستند و تنها پس از استفاده مشتری مشخص می گردند (برای مثال برخی از داروها). برای این موارد ایجاد یک حلقه بازخورد (Feedback Loop) که در آن اطلاعات میدانی برای بهبود فرآیندهای داخلی استفاده می شود، مهم است.

به طور خلاصه، درک کیفیت به معنای نگاه به خواست مشتری است و تحویل محصول مورد نظر مستلزم نگاه به تولید است. در ادامه این بخش تمرکز ما بر رابطه بین کیفیت و تولید، به ویژه اینکه چگونه این دو می توانند با هم به عنوان بخشی از فرآیند بهبود مستمر کارخانه همکاری کنند، خواهد بود.

کنترل کیفیت آماری (Statistical Quality Control)

کنترل کیفیت آماری (SQC) از طریق کنترل انطباق مشخصات (قابل اندازه گیری) محصول با استانداردهای فنی، بر کیفیت ساخت تمرکز دارد. هدف نهایی SQC کاهش سیستماتیک نوسانات و تغییرات در معیارهای کلیدی کیفیت است. به عنوان مثال، ابعاد و اندازه، وزن، تلرانس، قدرت، رنگ، سرعت، بو، طعم و … همه ویژگی‌های قابل اندازه‌گیری هستند که می‌توانند برای مشخص کردن کیفیت فرآیندهای تولید استفاده شوند.

رویکردهای SQC

ابزارهای مورد استفاده در SQC را برای اطمینان از کیفیت محصول به سه گروه تقسیم می شوند:

۱- نمونه گیری جهت پذیرش (Acceptance Sampling)؛ برای تعیین اینکه آیا محصولات تولید شده با مشخصات کیفی مطابقت دارند یا خیر اقدام به بازرسی و نمونه برداری می کنیم. در برخی شرایط نیاز است که کلیه محصولات تولیدی از نظر کیفی بازرسی شوند و در برخی موارد به نمونه برداری آماری اکتفا می کنیم. به عبارت دیگر بسته به شرایط اعم از هزینه، ضروری بودن کیفیت اقلام تولیدی، تخریب محصول برای بازرسی و .. با یک طیفی از نمونه برداری مواجه هستیم.

برای مثال، کارخانه های سازنده تلفن همراه معمولاً هر دستگاه را تحت چرخه ای از آزمایشات (اتوماتیک) قرار می دهند تا از عملکرد صحیح مدارت الکترونیکی و کنترل ها اطمینان حاصل می کند. در مقابل، یک کارخانه تولید مواد غذایی نمی تواند تک تک محصولات خود را تحت آزمایش طعم و مزه قرار دهد و باید برای اطمینان از کیفیت به نمونه برداری دوره ای تکیه کند.

توجه داشته باشید که بازرسی و نمونه گیری اساساً یک روش کنترلی در پایان خط تولید است (End-of-Line Method) و می تواند مشکلات را تنها پس از وقوع تشخیص دهد.

۲- کنترل فرآیند آماری (Statistical Process Control-SPC)؛ فرآیندهای تولید به طور پیوسته با توجه به انحراف معیار و میانگین، کنترل می شوند تا مشخص شود که چه زمانی مشکل خاصی رخ داده یا فرآیند از کنترل خارج شده است.

به عنوان مثال، در فرآیند آبکاری نیکل و کروم یا آنودایز آلومینیوم، نظارت و تنظیم دما، pH و سایر پارامترهای کنترلی در حمام های شیمیایی مهم است. اگر این موارد از سطوح مطلوب خارج شوند، ممکن است مشکلات کیفی مانند چسبندگی ضعیف و افت دوام ایجاد شود لذا اقدامات اصلاحی ضروری است.

SPC یک روش کنترلی در زمان است که مشکلات را در زمان وقوع (یا خیلی کوتاه پس از آن) شناسایی می‌کند و به این ترتیب می توان واکنش سریعی نسبت به رفع مشکل داشت.

۳- طراحی آزمایشات (Design of Experiments -DOE)؛ در این رویکرد علل مشکلات کیفی از طریق آزمایش‌های هدفمند مشخص و ردیابی می‌شوند. ایده اصلی، تغییر سیستماتیک و هدفمند متغیرهای قابل کنترل برای تعیین اثر آنها بر معیارهای کیفیت است. مجموعه ای از ابزارهای آماری (به عنوان مثال، طرح بلوک تصادفی، طرح فاکتوریل، روش تاگوچی و ..) برای ارتباط موثر کنترل با خروجی و بهینه سازی فرآیندها توسعه یافته اند.

روش طراحی آزمایشات، یک ابزار تشخیصی است که علت مشکلات کیفیت را قبل از شروع تولید شناسایی می کند و با این کار از وقوع آنها در آینده جلوگیری می کند. به طور معمول، زمانی که یک سازمان به بلوغ خودش رسیده باشد، کمتر به نمونه گیری و بازرسی پس از تولید می پردازد و بیشتر متکی به کنترل فرآیند آماری و طراحی آزمایشات برای بهبود مستمر می باشد.

از آنجا که کنترل فرآیند آماری (SPC) به طور خاص با رابطه بین کیفیت و نوسانات (تغییرات) در تولید سروکار دارد، تمرکز بیشتری بر این موضوع خواهیم داشت. پس از بحث و بررسی SPC، نشان می‌دهیم که چگونه شش سیگما به یک روش جامع کاهش نوسانات تبدیل شده است که مکملی عالی برای تئوری فیزیک کارخانه جهت بهبود مستمر است.

کنترل فرآیند آماری (Statistical Process Control)

کنترل فرآیند آماری (SPC) به طور کلی با یک ویژگی کیفی قابل اندازه گیری آغاز می شود. به عنوان مثال، قطر سوراخ در یک قطعه فولادی ریخته گری شده. صرف نظر از اینکه فرآیند ریخته گری چقدر کنترل می شود، همیشه مقدار مشخصی از تغییر در اندازه این قطر وجود خواهد داشت.

اگر تغییرات در اندازه نسبتاً کوچک و به دلیل محدودیت های فرآیندی غیرقابل کنترل باشد، آن را نوسان طبیعی (Natural Variability) می نامیم. فرآیندی که در نوسانات طبیعی خود به طور پایدار عمل می کند، اصطلاحاً تحت کنترل آماری (In Statistical Control) گفته می شود.

نوسانات و تغییرات بزرگتری که باید علت آن ریشه یابی شود، نوسان قابل انتساب یا قابل پیگیری (Assignable-Cause Variation) نامیده می‌شوند. گفته می‌شود فرآیندی که در معرض نوسانات قابل انتساب است، خارج از کنترل می باشد.

چالش اساسی SPC تفکیک علت تغییرات قابل انتساب از تغییرات طبیعی است. از آنجایی که ما عموماً فقط خود ویژگی کیفیت را مستقیماً مشاهده می کنیم و درباره علل تغییرات درکی نداریم، برای کسب اطلاعات در این مورد به آمار نیاز داریم. معرفی ابزارهای آماری و نمودارهای آن به فعالیت های ارزشمند شوهارت (Shewhart-1931) برمی گردد.

برای نشان دادن اصول اساسی SPC، اجازه دهید مثال کنترل قطر سوراخ در یک قطعه فولادی که توسط فرآیند ریخته گری ماسه ای ایجاد شده است را در نظر بگیریم. فرض کنید قطر اسمی مورد نظر ۱۰ میلی متر باشد و ما قطعه ای را با قطر ۱۰/۱ میلی متر مشاهده کنیم.

آیا می توانیم نتیجه بگیریم که فرآیند ریخته گری خارج از کنترل است؟ البته پاسخ این است: بستگی دارد؛ ممکن است انحراف ۰/۱ میلی متری در دامنه تغییرات طبیعی باشد. اگر اینطور بوده باشد و ما بخواهیم فرآیند را برای اصلاح این مقدار انحراف دوباره تنظیم کنیم (مثلاً با تغییر پارامترهای ریخته گری) به احتمال زیاد نتیجه بدتر می شود.

دلیل آن این است که تنظیم مجدد یک فرآیند در پاسخ به نویز تصادفی، نوسانات را افزایش می‌دهد. از این رو، برای اطمینان از اینکه تنظیمات فقط در پاسخ به نوسانات قابل انتساب انجام می شود، باید دامنه نوسانات طبیعی را مشخص کنیم.

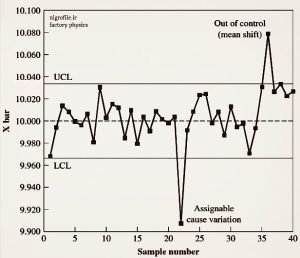
در مثال ما، فرض کنید تعدادی از قطعات ریخته‌گری‌ را اندازه‌گیری و مشخص می کنیم که با میانگین قطر ۱۰ و انحراف معیار ۰/۰۲۵ میلی متر قطعه تولیدی قابل قبول و تحت کنترل قرار دارد. بعلاوه فرض کنید که هر ۲ ساعت، یک نمونه تصادفی از پنج قطعه ریخته گری انتخاب و قطر سوراخ آنها را اندازه گرفته و میانگین را محاسبه می کنیم (Ẋ نامیده می شود) و آن را بر روی نموداری مانند نمودار نشان داده شده در شکل (۱) رسم می کنیم. از آمار اولیه می دانیم که خود Ẋ یک متغیر تصادفی است و دارای انحراف معیار است.

شکل ۱- نمودار کنترل کیفیت برای میانگین قطر سوراخ قطعات ریخته گری شده

$\sigma_{\bar{x}} = \frac{{\sigma}}{{\sqrt{n}}}$

که در آن n اندازه نمونه است. در این مثال n = 5 می باشد.

ایده اصلی پشت نمودارهای کنترلی بسیار شبیه به آزمون فرضیه (Hypothesis Testing) است. فرضیه صفر ما (Null Hypothesis) این است که فرآیند تحت کنترل است. یعنی نمونه ها از فرآیندی با میانگین μ و انحراف استاندارد σ بدست می آیند.

برای جلوگیری از اینکه تصور شود فرآیند خارج از کنترل است در حالی که اینطور نیست (خطای نوع یک) یک استاندارد سختگیرانه برای تعیین اینکه انحرافات واقعاً وجود داشته (که علل قابل انتساب و پیگیری هم نام گذاری کردیم)، تعیین می کنیم.

قرارداد استاندارد عبارت است از علامت گذاری نقاطی بیش از ۳ انحراف استاندارد بالاتر یا پایین تر از میانگین داده ها. ما این کار را با تعیین حد کنترل پایین و بالایی به صورت زیر انجام می دهیم:

$LCL = \mu - 3\sigma_{\bar{x}}$

$UCL = \mu + 3\sigma_{\bar{x}}$

اگر میانگین نمونه، خارج از محدوده بین LCL و UCL مشاهده شود، آنگاه این مشاهده به عنوان نوسان غیر عادی و قابل انتساب (پیگیری) تعیین می شود. در مثال قطعات ریخته گری که در شکل (۱) نشان داده شده است، چنین انحرافی در نمونه ۲۲ رخ داده است.

این ممکن است ناشی از ورودی های معیوب (مانند قطعه فولادی یا ماسه جهت ریخته گری)، مشکلات فرآیندی (ذوب ریزی)، یا خطای اپراتور باشد. SPC به ما نمی گوید که چرا این انحراف رخ داده است فقط هشدار می دهد که بررسی های بیشتری باید انجام پذیرد.

گاهی به جای یک نقطه، مجموعه ای از نقاط خارج (بالا یا پایین) از محدوده کنترلی هستند که باز هم برای تشخیص یک تغییر احتمالی در میانگین فرآیند استفاده می‌شود. در شکل (۱) نمونه ۳۷ خارج از کنترل است. اما بر خلاف نمونه ۲۲، این نقطه با یک دوره غیر معمول مشاهداتی بالاتر از حد متوسط در نمونه های ۳۵ تا ۴۰ همراه است.

این شواهد قوی نشان می دهد که علت این انحراف، منحصر به نمونه ۳۷ نیست، بلکه به دلیل چیزی در خود فرآیند ریخته گری است که باعث افزایش میانگین قطر شده است. شواهدی از این دست که تغییر در روند را به نشان می دهند (به عنوان مثال، یک روند سینوسی از افزایش و کاهش خارج از محدوده)، برای شناسایی تغییرات قابل انتساب استفاده می شود.

نکته مهم بعدی این است که تا اینجا معیار پذیرش ما مربوط به اندازه گیری خود قطعات بود. حدود کنترلی برای تک تک قطعات به ترتیب LNTL و UNTL (Lower and Upper Natural Tolerance Limits) نام دارد. همینطور برای میانگین نمونه گیری ها LCL و UCL بکار می رود.

برای پذیرش قطعات باید به حدود کنترلی که در استاندارها (یا حتی نیاز مشتری) آمده است توجه نمود. بنابراین منظور از LSL و USL (lower and an upper specification level) همین الزامات عملکردی است (در برخی متون Lower and Upper Warning Limit نامیده می شود).

در ادامه مثال قطعه ریخته گری اگر حدود کنترل تلرانس طبیعی داده ها به ترتیب زیر باشد:

LNTL = μ − ۳σ = 10 − ۳(۰/۰۲۵) = 9/۹۲۵

LNTL = μ + ۳σ = 10 + ۳(۰/۰۲۵) = 10/۰۷۵

و اگر فرض شود استاندارد (درخواست مشتری) حدود کنترلی را به شرح زیر تعیین نموده است:

LSL = LSL1 = 9/975

USL = USL1 = 10/025

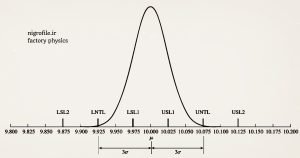
با ترسیم شکل (۲) و مشخص کردن حدود کنترلی بالا، مشخص می شود که کسر بزرگی از قطعات تولیدی نامنطبق (nonconforming parts) هستند. اگر قطر سوراخ قطعات تولیدی دارای توزیع نرمال باشند می توانیم درصد قطعات نامنطبق را بدست بیاوریم:

$\begin{flalign*} & \: P (9.975 \leq X \leq 10.025) = P(\frac{9.975-10}{0.025} \leq Z \leq \frac{10.025-10}{0.025}) &\\ & \: P (-1 \leq X \leq 1) = \phi (-1) + 1 - \phi (1)&\\ & \: = 0.1587 + 1 - 0.8413&\\ & \: = 0.3174 &\\ \end{flalign*}$

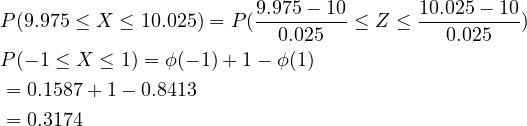
برابر نتیجه بدست آمده ۳۲ درصد قطعات با استاندارد داده شده مطابقت ندارند. در عوض فرض کنید اینبار حدود کنترلی به ترتیب برابر LSL = LSL2 = 9/875 و USL = USL2 = 10/125 داده شده باشد. از آنجایی که تلرانس طبیعی قطعات در این محدوده قرار دارند، انتظار داریم قطعات نامنطبق بسیار کمی داشته باشیم.

شکل ۲- مقایسه حدود کنترل با استفاده از تلرانس طبیعی فرآیند و حدود استاندارد یا الزامات عملکردی

در واقع، تکرار محاسبه بالا برای این حدود نشان می دهد که کسر قطعات نامنطبق ۰/۰۰۰۰۰۰۵۷ خواهد بود.

برای شناخت بهتر فرآیند از این نظر که آیا می تواند الزامات عملکردی را پاس کند یا خیر از شاخص قابلیت فرآیند (C_PK) که به صورت زیر تعریف می شود استفاده می کنیم:

$C_{pk} = \frac{Z_{min}}{3}$

$Z_{min}= min\{-Z_{LSL}, Z_{USL}\}$

$Z_{LSL} = \frac{LSL-{\mu}}{\sigma}$

$Z_{USL} = \frac{USL-{\mu}}{\sigma}$

حداقل قابل قبول برای این شاخص برابر یک است. برای همین مثال قطعات ریخته گری محاسبات این شاخص برابر است با:

$C_{pk} = \frac{1}{3} \text{for (LSL1,USL1)}$

$C_{pk} = \frac{5}{3} \text{for (LSL2,USL2)}$

واضح است که برای حدود کنترلی (LSL1- USL1) این شاخص کمتر از یک می باشد و تأییدی بر خارج از کنترل بودن فرآیند دارد که قبلاً مشاهده کرده بودیم.

برای اجرای SPC موثر، باید به مجموعه ای از جزئیات پرداخته شود. برای مثال باید اندازه نمونه (n) مناسب انتخاب شود و به اندازه کافی بزرگ باشد تا اثرات نوسانات و نویز ورودی خنثی شود، ثانیاً آنقدر هم بزرگ نباشد که تغییرات و نوسانات غیر طبیعی را پنهان کند. فرکانس و تعداد دفعات نمونه برداری هم مهم است و باید یک تعادلی از هزینه و دقت داشته باشیم.

توسعه مفهوم کنترل فرآیند آماری (SPC Extensions)

نمودار Ẋ که تا مورد بحث قرار گرفت تنها یکی از نمودارهای SPC است که بیشتر برای داده هایی مفید است که از توزیع نرمال تبعیت می کنند. برای نیازهای تضمین کیفیت نمودارهای دیگری نیز گسترش یافته اند. چند مورد که در مدیریت تولید مفید هستند عبارتند از:

نمودار R؛ در این نمودار به جای میانگین از اختلاف بین بزرگترین با کوچک ترین داده استفاده می شود. اگر x_۱, x_۲, . . . , x_n نشان دهنده مقادیر اندازه گیری شده باشند (برای مثال قطر سوراخ قطعات ریخته گری) در یک نمونه n تایی، آنگاه دامنه تغییرات (R) به صورت زیر تعریف می شود:

$R = X_{max}-X_{min}$

با هر بار نمونه گیری می توان یک نمودار R تهیه کرد. و از چند نمونه گیری Ṙ (میانگین R) به دست می آید که در تعیین حدود کنترلی به شرح زیر بکار می رود:

$LCL = \bar{R}-3\sigma_{R}$

$UCL = \bar{R}+3\sigma_{R}$

اگر نمودار R نقاط خارج از کنترل نداشته باشد، بدین معنی است که نوسانات فرآیند به اندازه کافی برای اعمال نمودار Ẋ پایدار می باشد. اغلب، نمودارهای Ẋ و R به طور همزمان اعمال می شوند تا تغییرات در میانگین یا واریانس فرآیند به طور دقیق تری بررسی شود.

نمودار نسبت اقلام معیوب و نامنطبق (p-charts)؛ یک قطعه یا محصول به دو صورت سالم یا معیوب قابلیت تولید دارد. الزامات و استاندارد های کیفیت در این نمودار اغلب از نوع وصفی (کیفی) است مثل طعم یک ماده غذایی که می تواند خوب یا بد در نظر گرفته شود. چون دو حالت بیشتر نداریم تعداد اقلام نامنطبق دارای توزیع دو جمله ای خواهد بود. حدود کنترلی در این نمودار عبارت است از:

$LCL = P - 3 \sqrt {\frac {P(1-P)}{n}}$

$UCL =P + 3 \sqrt {\frac {P(1-P)}{n}}$

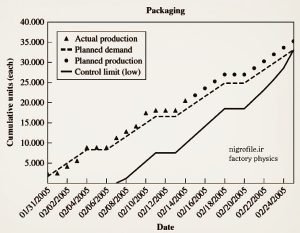
کاربردهایی غیر از کنترل کیفیت (Nonquality applications)؛ منظور این است که می توان از نمودارهای کنترل کیفیت برای بخش های دیگر از جمله تولید نیز استفاده کرد. برای مثال در شرکت های که برنامه ریزی تولید بر اساس سفارشات دریافتی از واحد فروش انجام می شود می توان گراف (تجمعی) سفارشات مشتریان و مقادیر تولید شده را بر حسب زمان در یک نمودار ترسیم کرد و با تعیین حدود کنترلی (۳σ -) برنامه تولید را ردیابی نمود.

شکل ۳- مثالی از کاربرد نمودار کنترل کیفیت در پایش عملکرد تولید

قدرت و انعطاف پذیری نمودارهای کنترلی، آنها را برای نظارت بر انواع فرآیندهایی که دارای نوسانات هستند، بسیار مفید می کند. از آنجایی که تقریباً تمام فرآیندهای تولید شامل نوسان هستند، تکنیک‌های SPC بخشی اساسی از ابزار مدیریت تولید پیشرفته می باشد.

شش سیگما (Six Sigma)

اصطلاح “شش سیگما” توسط شرکت موتورولا برای توصیف شیوه های کنترل کیفیت شرکت در دهه ۱۹۸۰ ابداع شد .شش سیگما که در ابتدا به عنوان یک روش آماری برای کاهش نقض و عیوب به سطوح بسیار پایین (قسمت در میلیون) در نظر گرفته شد، به تدریج به یک سیستم مدیریت کیفیت جامع تبدیل شد که دارای یک روش حل مسئله و ساختار سازمانی بود.

در دهه ۱۹۹۰ سایر شرکت‌ها، به‌ویژه جنرال الکتریک و Allied Signal، شش سیگما را از کف کارخانه به سطح مدیریت اجرایی ارتقا داده و به عنوان یک سیستم مدیریت جامع با محوریت کاهش نوسانات در تمام فرآیندهای تجاری خود نظر گرفتند.

مبانی آماری شش سیگما (Statistical Foundations)

هسته شش سیگما مدلی است که نوسانات و تغیرات فرآیند را به عیوب مرتبط می کند. در واقع، این همان نمودارهای SPC است که یک توزیع نرمال با میانگین μ و انحراف استاندارد σ را در نظر می گیرد و بعد بررسی می کند که فرآیند مورد نظر (که البته باید قابل اندازه گیری باشد) چقدر با این توزیع نرمال متفاوت است.

همانطور که در شکل (۲) اشاره کردیم، مقدار و کسر قطعات معیوب و نامنطبق به حدود مشخصات و استانداردهای مربوطه (Specification Limits) بستگی دارد. هر چه این حدود (USL-LSL) بزرگتر باشد، احتمال وجود قطعات معیوب کمتر است. مدل شش سیگما فاصله مشخصات کنترلی را در واحد σ اندازه گیری کرده و از توزیع نرمال برای محاسبه تعداد قطعات (خروجی) معیوب استفاده می کند.

این مفهوم را دوباره با همان مثال قطعات ریخته گری نشان می دهیم. فرض کنید تعیین کرده‌ایم که تا زمانی که قطر سوراخ قطعات ریخته گری شده بین ۹/۹۵ تا ۱۰/۰۵ میلی‌متر باشد، قطعات تولیدی قابل استفاده است. در اصطلاح SPC این بدان معنی است که فاصله مشخصات با = (۹/۹۵-۱۰/۰۵ = LSL-USL) داده شده و دارای نیم عرض (half-width) 0/05 میلی متر است (نیم عرض یعنی از میانگین که اینجا ۱۰ است تا یک طرف مثلاً ۱۰/۰۵ مقدار فاصله برابر ۰/۰۵ است).

فرض کنید فرآیند مثال ما، قطعاتی تولید می‌کند که قطر آنها به طور معمول با میانگین ۱۰ میلی‌متر و انحراف استاندارد σ = 0/۰۲۵ میلی‌متر می باشد. از آنجائیکه میانگین این قطعات کاملاً با میانگین بازه مشخصات و استاندارد داده شده، منطبق است به این فرآیند ریخته گری یک فرآیند متمرکز (Centered Process) گفته می شود.

اما در مورد انحراف معیار چی باید گفت؟ در بالا، مقدار استاندارد داده شده دارای نیم عرض برابر ۰/۰۵ میلی متر است که معادل دو برابر انحراف معیار قطعات تولیدی است لذا به این فرآیند دو سیگما می گویند چراکه (۲σ = 2(۰/۰۲۵) = 0/۰۵ millimeters).

اگر بازه مشخصات و استاندارد داده شده بجای مقدار قبلی برابر با (۹/۹۲۵-۱۰/۰۷۵ = LSL-USL) باشد، دوباره میانگین ها که کاملاً بر هم منطبق هستند ولی انحراف معیار بازه جدید ۳ برابر انحراف معیار قطعات تولید شده است (۳σ = 3(۰/۰۲۵) = 0/۰۷۵ millimeters) بنابراین ما یک فرآیند سه سیگما داریم.

در نهایت اگر استاندارد داده شده که می تواند درخواست مشتری را هم شامل شود، برابر با (۹/۸۵۰-۱۰/۱۵۰ = LSL-USL) باشد ما یک فرآیند شش سیگما خواهیم داشت (۶σ = 6(۰/۰۲۵) = 0/۱۵ millimeters).

حالا از این مفهوم چه جوری برای تعیین مقدار مورد انتظار خرابی ها استفاده کنیم؟ شکل ۴ (a، b، c) نشان می دهد که چگونه این مفهوم شش سیگما برای محاسبه جهت تعیین نرخ عیوب استفاده می شود.

در یک فرآیند k-sigma متمرکز (یعنی میانگین فرآیند منطبق بر میانگین استاندارد داده شده اما دارای انحراف معیار کوچتری به میزان K است)، تعداد قطعات معیوب (خروجی نامطلوب) برابر است با کسری از مساحت زیر یک توزیع نرمال که k سیگما بالاتر یا پایین تر از میانگین قرار دارد. برای فرآیند یک سیگما، این تقریباً ۳۲ درصد است. برای فرآیند دو سیگما حدود ۵ درصد و برای فرآیند سه سیگما کمتر از ۱ درصد می باشد.

برای یک فرآیند شش سیگما (متمرکز)، کسر خروجی های نامطلوب کمتر از ۲ در یک میلیارد است که ممکن است ناممکن و دست نیافتنی به نظر برسد. چه فرآیندهایی را می توان یک میلیارد بار انجام داد (یا یک میلیارد بار اتفاق بیفتد) و در عین حال کمتر از دو خطا داشته باشد؟ یه چند آمار را باهم مرور می کنیم:

نرخ تصادفات مرگبار در سفرهای هوایی تجاری (برخورد دو هواپیما در آسمان) حدود ۰/۱۷ در هر ۱,۰۰۰,۰۰۰ (۱۷۰ در میلیارد) است. میزان مرگ و میر در سفر با قطار تقریباً ۱/۶ مرگ در هر میلیون سفر (۱۶۰۰ در میلیارد) می باشد.

نرخ مرگ و میر نوزادان در ایالات متحده حدود ۷ در ۱۰۰۰ تولد (۷,۰۰۰,۰۰۰ در هر میلیارد) است. حتی با وجود واکسیناسیون آبله میزان مرگ و میر حدود ۱ در ۱,۰۰۰,۰۰۰ (۱۰۰۰ در میلیارد) است. حتی موارد طبیعی از جمله مرگ و میر در اثر نیش زنبورها نیز بالاتر از این عدد است، تقریباً ۰/۲ نفر در هر میلیون (۲۰۰ نفر در میلیارد) هر سال در ایالات متحده بر اثر نیش زنبور می میرند.

همانطور که ملاحظه فرمودید اگر بخواهیم که میانگین فرآیند دقیقاً متمرکز و برابر استانداردها باشد عملاً تعداد عیوب به خصوص در حالت شش سیگما بسیار ناچیز است و به درد هدف گذاری در بحث کیفت نمی خورد.

بنابراین مدل زیربنایی مورد استفاده در شش سیگما فرض را بر این گذاشته است که میانگین نمونه ها با میانگین استاندارد ۱/۵ انحراف معیار فاصله دارد و به جای فرآیند متمرکز یک فرآیند شیفت یافته را در نظر می گیرد. با اینکار هرچند تعداد عیوب احتمالی افزایش می یابد اما قابلیت هدف گذاری خواهد داشت.

شکل (۴) مربوط به همان مثال قطعات تولید شده در فرآیند ریخته گری است این مفهوم را به خوبی توضیح می دهد. جهت یادآوری، در این مثال قطعات تولیدی دارای توزیعی با میانگین ۱۰ و انحراف استاندارد برابر ۰/۰۲۵ میلیمتر هستند.

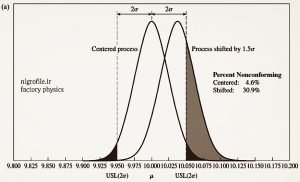
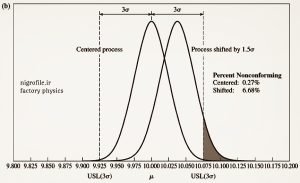
اگر بازه استاندارد داده شده برابر با (۱۰/۰۵-۹/۹۵) باشد و میانگین قطعات تولیدی با میانگین این استاندارد یکسان و برابر با ۱۰ باشد (فرآیند متمرکز) گفته شد که در موقعیت دو سیگما هستیم، آنگاه میزان عیوب مورد انتظار تقریباً برابر ۵ درصد خواهد بود. اما شش سیگما فرض می کند که میانگین فرآیند نه تنها با میانگین استاندارد یکسان نمی باشد بلکه ۱/۵ سیگما هم انحراف دارد.

همانطور که در شکل ملاحظه می کنید در این حالت میانگین قطعات تولیدی در نقطه ۱۰/۰۳۷۵ قرار می گیرد زیرا : ۰/۰۳۷۵= (۰/۰۲۵) ۱/۵ در نتیجه احتمال تولید قطعات نامنطبق افزایش یافته و به حدود ۳۱ درصد می رسد. همین تجزیه و تحلیل برای حالتیکه در موقعیت سه و شش سیگما هستیم در شکل های b و c به ترتیب نشان داده شده است.

شکل 4a – درصد احتمال خروجی نامنطبق (نامطلوب) در حالت متمرکز و شیفت یافته برای دو سیگما

شکل 4b – درصد احتمال خروجی نامنطبق (نامطلوب) در حالت متمرکز و شیفت یافته برای سه سیگما

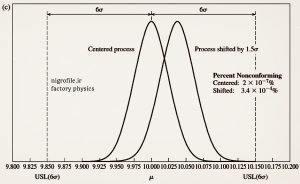
شکل 4c – درصد احتمال خروجی نامنطبق (نامطلوب) در حالت متمرکز و شیفت یافته برای شش سیگما

به شکل ۴-ج که مربوط به حالت شش سیگما است دقت کنید. در حالتیکه که میانگین فرآیند متمرکز است احتمال خروجی نامنطبق ۲ در میلیارد است اما در حالت شیفت یافته این احتمال برابر (^۴-۱۰ × ۳/۴) یا به مفهوم بهتر ۳/۴ قطعه در میلیون می باشد و این همان هدف نهایی شش سیگما است که در بیشتر متون آمده است و از نتیجه به بعد راجع به شش سیگما صحبت می کنند.

دقت داشته باشید وقتی گفته می شود ۳/۴ قطعه در میلیون در رابطه با یک کسر صحبت می کنیم که در صورت آن ۳/۴ و در مخرج یک میلیون قرار دارد و این یعنی هم می توانید جهت بهبود فرآیند خود صورت کسر را کوچک نمایید، یا مخرج کسر را بزرگتر کنیم تا حاصل کسر کوچکتر شود.

شش سیگما زمانی یک راه معقول برای اندازه‌گیری پیشرفت در بهبود نسبی کیفیت است که مخرج کسر ثابت و سعی داشته باشیم مقدار صورت کسر که مرتبط با خرابی ها است را کوچکتر نماییم. خلاصه اینکه در تفسیر و بکارگیری این روش دقت کنید.

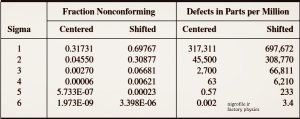
جدول ۱- خلاصه محاسبات مربوط به احتمال و مقدار خروجی نامطلوب در مدل شش سیگما

در جدول (۱) احتمال، تعداد عیوب و موارد نامنطبق مورد انتظار، برای فرآیند یک تا شش سیگما در دوحالت متمرکز و شیفت یافته آمده است که می تواند اطلاعات مفیدی برای خواننده کنجکاو داشته باشد.

روش DMAIC

دلیل اصلی کاربرد گسترده شش سیگما در ارائه چارچوب و توسعه ابزارهایی به منظور دستیابی به بالاترین استاندارد کیفیت نهفته است. بسته به سازمان، پیاده‌سازی شش سیگما می‌تواند شامل روش های نظارت و بهبود کیفیت، از نمودارهای کنترل تا حلقه‌های کیفیت باشد (منظور از حلقه های کیفیت همان Plan, Do, Check, Act).

تمرکز اصلی همه برنامه های شش سیگما، بر جمع آوری داده ها و تجزیه و تحلیل آنها است. برخلاف برخی از رویکردهای کیفی “نرم” در دوران اوج جنبش TQM در دهه ۱۹۸۰، که بر پیشنهادات و جلسات طوفان فکری متمرکز بودند، رویکرد شش سیگما بیشتر بر تجزیه و تحلیل آماری تکیه دارد.

ابزار اصلی اصلی شش سیگما برای هدایت برنامه های کنترل کیفیت جهت دستیابی به نرخ عیوب ۳/۴ قسمت در میلیون، DMAIC نامیده می شود که مخفف عبارت زیر است :

Define : مشخص کنید که چه فرآیندی باید بهبود یابد.

Measure : عملکرد فعلی را اندازه گیری نمایید.

Analyze : چه زمانی، کجا و چرا نقص در کیفیت ایجاد شده است.

Improve : تلاش برای حذف یا به حداقل رساندن علل ایجاد عیوب.

Control : کنترل فرآیند بعد از انجام اقدامات اصلاحی.

این چارچوب برای فرآیندهای موجود که نیاز به بهبود دارند مناسب است. برای فرآیندهایی که هنوز وجود ندارند، یا نیاز به طراحی مجدد دارند (به عنوان مثال، DMAIC اعمال شده است ولی کیفیت هنوز نیازهای مشتری یا هدف شش سیگما را برآورده نمی کند)، یک نوع از DMAIC، به نام DMADV، توسعه داده شده است :

Define : اهداف پروژه را مشخص کنید.

Measure : نیازها و مشخصات مورد نظر مشتریان را جمع آوری کنید.

Analyze : جنبه های فرآیندی را که می تواند نیاز مشتریان را برآورده نماید مورد بررسی قرار دهید.

Design : فرآیند مطلوب را برای رفع نیاز مشتری طراحی کنید.

Verify: بررسی فرآیند طراحی شده بر اساس توانایی آن در تحقق اهداف مورد نظر.

همانطور که ملاحظه می نمایید مفاهیم DMAIC و DMADV به عنوان ابزار اساسی تحلیل سیستم‌ها معرفی شده اند. این ابزارها با تأکید زیادشان بر اندازه‌گیری کمی عملکرد، یک مکانیسم حل مسئله ساختاریافته ارائه می‌کنند (Structured) که می‌تواند تقریباً برای هر جنبه‌ای از یک کسب‌وکار اعمال شود.

ساختار سازمانی (Organizational Structure)

سوالی که معمولاً با درک رویکرد شش سیگما مطرح می شود این است که چرا شش سیگما با اینکه ترکیبی از گام های معمولی است، اینقدر تأثیرگذار است؟

یک پاسخ می تواند این باشد که شش سیگما یک درمان بسیار مؤثر بود. بسیاری از نوآوری ها در کسب و کار (همانند مدل کسب و کار شرکت کامپیوتر Dell) بیشتر مدیون ترکیب موفقیت آمیز و البته هوشمندانه از مفاهیم موجود است تا ایجاد تغییرات انقلابی در حوزه های گوناگون. ترکیب یک معیار عملکرد کمی دقیق با یک فرآیند تجزیه و تحلیل ساختاریافته مطمئناً قدرتمند است.

علت دیگر برای موفقیت شش سیگما، ساختار سازمانی است که برای اجرای این فرآیندها استفاده می‌کند. به عنوان یک برنامه بهبود فرآیند، شش سیگما پنج نقش سازمانی را تعریف می کند:

رهبری اجرایی (Executive leadership)؛ شامل مدیرعامل و سایر مدیران ارشد است. در حالی که به طور رسمی بخشی از ساختار تیم شش سیگما نیستند، اما مسئول ایجاد چشم انداز و توانمندسازی سایر کارکنان هستند. موفقیت شش سیگما در شرکت هایی مانند موتورولا، جنرال الکتریک به شدت به حمایت و مشارکت مدیران ارشد وابسته بود.

قهرمانان (Champions)؛ رهبرانی هستند که مسئولیت روزانه اجرای شش سیگما در سراسر سازمان را بر عهده دارند، معمولاً از رده‌های بالای مدیریتی انتخاب می‌شوند و به عنوان مربی برای کمربندهای سیاه (Black belts) عمل می‌کنند. لازم به ذکر است در رویکرد شش سیگما سعی شده است تا عناوین جذابی به هریک از نقش ها داده شود و ممکن است بین شرکت‌ها متفاوت باشد (به عنوان مثال، جنرال الکتریک از اصطلاح «رهبران کیفیت» استفاده کرده است).

کمربندهای مشکی استاد (Master black belts)؛ توسط قهرمانان شناسایی می شوند و به عنوان مربیان متخصص در سازمان و برای تحقق پروژه شش سیگما خدمت می کنند. بر خلاف رهبران اجرایی و قهرمانان، کمربندهای مشکی استاد تمام وقت خود را به شش سیگما اختصاص می دهند. آنها به قهرمانان کمک می کنند و کمربند سیاه و سبز را راهنمایی می کنند. این نقش مستلزم توانایی بالا در زمینه آمار و مهارت های مدیریتی است. اغلب زمان آنها صرف اطمینان از استقرار یکپارچه شش سیگما در بخش ها و فرآیندهای مورد نظر سازمان می شود.

کمربندهای سیاه (Black belts)؛ تحت نظر کمربندهای سیاه استاد عمل می کنند تا روش شش سیگما را در پروژه های خاص اعمال کنند. آنها نیز تمام وقت خود را به شش سیگما اختصاص می دهند. تمرکز اصلی آنها بر روی اجرا و پیاده سازی پروژه شش سیگما است، برخلاف قهرمانان و کمربندهای مشکی استاد که بر شناسایی فرصت های بکارگیری شش سیگما تمرکز دارند.

کمربندهای سبز (Green belts)؛ کارکنانی هستند که اجرای شش سیگما را در کنار سایر مسئولیت های شغلی خود انجام می دهند به عبارت دیگر تمام وقت درخدمت پروژه نیستند. آنها معمولاً تحت هدایت کمربندهای سیاه عمل می کنند و آنها را جهت دستیابی به نتایج مورد نظر حمایت می کنند.

شش سیگما با ایجاد این نقش‌ها (عناوین) و نهادینه کردن آن‌ها از طریق آموزش مستمر و دقیق، کارکنانی را پرورش می‌دهد که علاوه بر توانایی فنی بالا، پروژه ها را تا حصول موفقیت نهایی دنبال می کنند. بنابراین، بر خلاف برخی دیگر برنامه های مشابه که با یک دوره کوتاه به پایان می رسد، شش سیگما این مزیت را دارد که توسط پرسنل تمام وقت طرح ریزی و اجرا شود. عناوین کمربند مشکی استاد و کمربند مشکی و سبز به قدری گسترده و فراگیر شده است که بسیاری از افراد آن را در رزومه و حتی کارت ویزیت خود درج می کنند.

از نقطه نظر برنامه ریزی و عملیات تولید، شش سیگما یک رویکرد قدرتمند جهت کاهش تغییرات و نوسانات است. همانطور که قبلاً بحث کردیم، چنین نوساناتی می‌تواند نتیجه مسائل کیفیت، خطای اپراتور، مشکلات تامین‌کننده، قابلیت اطمینان محصول یا هر مشکل دیگر باشد. هنگامی که یک مشکل شناسایی شد، روش شش سیگما را می توان برای شناسایی علت و رفع آن بکار گرفت.

با این حال توجه داشته باشید که علی رغم نقاط قوت آن، در پیش‌بینی مکان‌هایی که احتمال وقوع نوسانات و تغییرات وجود دارد چندان خوب نیست. دلیل آن هم این است که شش سیگما از یک مدل آماری و تحلیل سیستم های عمومی استفاده می کند و در نتیجه می بایست به عنوان مکمل همراه با روش های دیگر به کار گرفته شود.

کیفیت

کنترل کیفیت آماری (SPC – Six Sigma)

بخش هفدهم؛ کنترل کیفیت آماری (Statistical Quality Control)

دوره های گذشته در کیفیت (The Decade of Quality)