بهمن
برنامه ریزی تولید
محاسبات کاربردی در برنامه ریزی تولید؛ اثر نوسانات بر تولید
بخش هشتم: اثر نوسانات بر تولید (EFFECT OF VARIABILITY)
نوسانات و تغییرات در اطراف ما وجود دارد. در همه جای یک کارخانه ی تولیدی اثر نوسانات و عوامل تصادفی قابل مشاهده است. تغییر در تقاضا و تأمین مجدد کالا برای انبار قبلاً مورد بحث قرار گرفت. اما در فرآیند تولید (Processing) نیز نوسانات حضور دارند. حالا سوال این است که اثر نوسانات بر تولید چیست؟
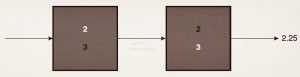
یک کارشناس برنامه ریزی ممکن است فکر کند، خوب نوسانات وجود دارد. من فقط از میانگین زمان فرآیند استفاده خواهم کرد و متوسط عملکرد را دنبال خواهم کرد اما متأسفانه این روش کار نمی کند. یک خط تولید با دو ایستگاه کاری را در نظر بگیرید که نیمی از زمان تولید آن سریع (سه واحد در دقیقه) و نیمی دیگر کند است (دو واحد در دقیقه). در ظاهر میانگین نرخ تولید برابر ۲.۵ واحد در دقیقه است.
اما همه داستان این نیست. اگر هر دو دستگاه سریع باشند، در نتیجه خروجی سریع خواهد بود. اما اگر ماشین اول سریع باشد اما ماشین دیگر کند باشد، خروجی کند است (تولید ماشین اول توسط ماشین دوم مسدود می شود). به همین ترتیب، اگر ماشین اول کند باشد اما ماشین دوم سریع باشد، خروجی باز هم کند است (ماشین دوم توسط ماشین اول به تعداد کافی تغذیه نمی شود). در نهایت اگر هر دو ماشین کند باشند، خروجی هم کند است.
هر یک از این چهار سناریو احتمال وقوع یکسان و برابر با ۰/۲۵ دارند. بنابراین در ۰/۷۵ مواقع نرخ تولید ۲ واحد در دقیقه و در ۰/۲۵ اوقات ۳ واحد در دقیقه می باشد در نتیجه متوسط نرخ تولید ۲/۲۵= (۰/۷۵ × ۲) + (۰/۲۵ × ۳) واحد در دقیقه است. نتیجه اینکه هر زمان که نوسانات وجود داشته باشد، عملکرد یک خط تولید کاهش می یابد.
دربخش های قبلی در مورد نیاز به حضور بافرها در کنار نوسانات صحبت کردیم. رفتار طبیعی عملیات تولید به گونه ای است که در صورت وجود ظرفیت اضافی، زمان انتظار نباید طولانی باشد. فرض کنید که سیستم نشان داده شده در شکل (۱) تقاضای یک واحد (قطعه) در ساعت دارد (به یاد داشته باشید که ظرفیت ۲.۵ واحد در دقیقه است).
شکل ۱- یک خط تولید با دو ایستگاه و عوامل تصادفی در تولید
در این سیستم تولیدی با نرخ تقاضای یک قطعه در ساعت هرگز صف وجود نخواهد داشت زیرا برای تولید با این نرخ، سیستم همیشه خالی است. اما اگر قطعات با سرعت یک واحد در دقیقه می رسیدند، سیستم با گذشت زمان یک صف طولانی ایجاد می کرد. گفته می شود که چنین سیستمی ناپایدار است زیرا در نهایت از کار خواهد افتاد. در واقع، حتی سیستم هایی که در آنها تقاضا برابر با ظرفیت است، در دراز مدت، ناپایدار هستند. علت عوامل تصادفی یا همان نوسانات است.
به طور کلی اگر Ci,j به معنی زمان تکمیل jامین کار روی ماشین iام باشد و Pi,j نیز برابر با زمان تکمیل فرآیند jام در این ماشین نظر گرفته شود آنگاه این زمان تکمیل برابر است با:
![\[ C_{i,j}=max \{C_{i,j-1}, C_{i-1,j}\}+P_{i,j}\]](https://nigrofile.ir/wp-content/ql-cache/quicklatex.com-7d33b2f0ff630759351e666d31800c22_l3.png "Rendered by QuickLaTeX.com")
هیچ کاری روی قطعات نمی تواند شروع شود تا زمانی که اولاً قطعه وارد ماشین شود و در ثانی فرآیند قطعه قبلی به پایان رسیده باشد و اگر قطعه قبلی همچنان در حال تکمیل باشد فرآیند قطعه جدید ورودی نمی تواند آغاز شود. به بیان ساده تر زمان تکمیل فرآیند یک قطعه شامل مدت زمان کار ماشین روی قطعه به اضافه مدت زمان انتظار برای دریافت خدمت است که در مجموع باعث می شود زمان تکمیل یک متغیر تصادفی باشد. در ادامه دلیل تشکیل صف در خط تولید به فرم زیر تعریف می شود:
![\[ E[max\{X,Y\}] \geqslant max\{E[X],E[Y]\}\]](https://nigrofile.ir/wp-content/ql-cache/quicklatex.com-e7c4c8a3b859ebf06ecb4202d7fd9eff_l3.png "Rendered by QuickLaTeX.com")
معنی رابطه فوق این است که مقدار مورد انتظار (میانگین) برای ماکزیمم دو متغیر تصادفی اغلب بزرگتر از ماکزیمم مقادیر مورد انتظار خواهد بود. برای مثال مقدار مورد انتظار برای پرتاب یک تاس ۳/۵ است، اما وقتی دو تاس ریخته می شود، مقدار مورد انتظار حداکثر دو تاس تقریباً برابر ۴/۵ است که از ۳/۵ بزرگتر می باشد. این مفهوم مهمی است و به نوعی اثر هم افزایی البته در جهت منفی بر خط تولید را نشان می دهد.
ردیابی نوسانات (Tracking of Variability)
برای مشاهده اثر تغییرات و نوسانات بر وضعیت تولید شرکت خود می توانید از نمودارهایی شبیه به آنچه که در این قسمت معرفی می شود استفاده کنید. این نمودارها را می توان به سادگی ترسیم و به یک شهودی از مفهوم نوسانات رسید. هرچه داده های مرتبط با تولید غنی باشد نتیجه بهتری خواهید گرفت.
اکثر شرکت ها در پایان دوره برنامه ریزی خود (معمولاً هفتگی یا ماهانه)، میزان انحراف از تولید، یعنی اختلاف بین آنچه که باید تولید می کردیم و آنچه در عمل تولید شده است را ثبت می کنند. اگر داده های مربوط به مقادیر انحراف از تولید را در قالب یک سری زمانی ترسیم کنیم و مشاهده کنیم که نمودار صعودی است این یعنی وضعیت تولید چندان مناسب نیست.
نمودار های دیگری نیز هستند که در کنار انحراف از تولید می توانند اطلاعات مفیدی ارائه نمایند. اولین نمودار شامل ترسیم سری زمانی میانگین تولید ماهانه یا هفتگی (بر اساس دوره برنامه ریزی) است. اگر اطلاعات دوره های برنامه ریزی برای حداقل ۳ تا ۵ سال اخیر را داشته باشید، میانگین تولید را استخراج و به صورت نمودار نمایش دهید. اگر روند داده ها صعودی باشد نشان می دهد که در بحث ظرفیت و توان عملیاتی اقدامات مثبتی انجام شده است.
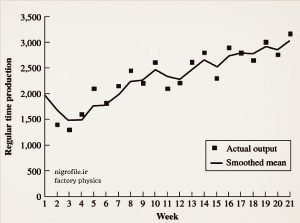
شکل ۲- سری زمانی میانگین تولید در دوره برنامه ریزی
شکل (۲) نمونه ای از چنین نموداری را نشان می دهد که افق برنامه ریزی آن هفتگی است. داده های میانگین تولید همراه با میانگین هموار شده (smoothed mean) ترسیم شده است. اما همان ترسیم داده های تولید به همراه خط روند (Trend Line) که در اکسل براحتی قابل انجام است نیز نتیجه یکسانی خواهد داشت. هدف این است که ببینیم آمار تولیدمان صعودی بوده یا نزولی. در گام بعد این بار نمودار سری زمانی واریانس یا انحراف معیار مقادیر تولید شده در دوره برنامه ریزی را ترسیم کنید (شکل ۳ را ببینید).
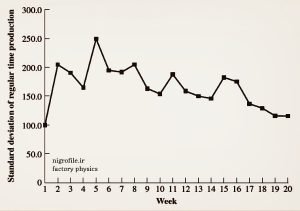
شکل ۳- سری زمانی انحراف معیار داده های تولید
در این شکل مشخص است که انحراف معیار مقادیر تولید شده نزولی بوده و به معنای دیگر نوسانات تولید تا حد زیادی تحت کنترل قرار دارد. اگر وضعیت تولید شما نیز مطابق این تصاویر است که خوش به حالتان و با همین فرمون ادامه بدهید اما اگر نمودارهای میانگین و انحراف معیار تولید هر دو صعودی هستند باید ادامه مطالب را با دقت بیشتری دنبال کنید.
اندازه گیری نوسانات (Measures of Variability)
در آمار، میانگین مجموعه ای از اعداد تصادفی برای نشان دادن تمایل به مرکز داده ها محاسبه می شود و انحراف استاندارد یا واریانس نیز میزان پراکندگی در داده ها را نشان می دهد. قبلاً، هنگام بحث در مورد تقاضا، میانگین (d) و واریانس (σd۲) را برای مشخص کردن تقاضا محاسبه کردیم و همچنین نسبت واریانس به میانگین (variance-to-mean ratio- VMR) برابر σd۲/d تعریف کردیم که اطلاعاتی در مورد نوسانات تصادفی ارائه می دهد. به نظر می رسد که مقدار VMR می تواند در تولید به صورت دسته ای (Batch) افزایش یابد.
به عنوان مثال، اگر تقاضا دارای توزیع پواسون باشد (یعنی واریانس تعداد تقاضا برابر با میانگین تعداد تقاضا است) اما هر تقاضا برای ۱۰۰ واحد باشد، VMR برابر یک نمی باشد بلکه ۱۰۰ خواهد بود. زیرا تقاضای واقعی اغلب بزرگتر از یک واحد است در نتیجه نسبت واریانس به میانگین هم مقدار بزرگتری می باشد، حتی اگر تعداد تقاضاها دارای توزیع پواسون باشد.
هنگام بحث در مورد نوسانات زمان فرآیند، ما کاری مشابه انجام می دهیم. میانگین زمان فرآیند را محاسبه کنید و آن را به صورت (T) یا (te) نشان می دهیم. ما از اندیس e برای نشان دادن زمان موثر فرآیند استفاده می کنیم. موثر به این معنی است که تمام اجزای زمان فرآیند، از جمله زمان واقعی انجام کار، زمان راهاندازی، زمان توقف، کار مجدد و غیره در نظر گرفته میشوند.
به همین ترتیب، واریانس (σ۲) یا (σe۲) است. در نهایت، مجذور ضریب تغییرات (Squared Coefficient of Variation) برای مشخص کردن تصادفی بودن زمانهای فرآیند مؤثر محاسبه میشود. همانطور که در جدول (۱) نشان داده شده است، نوسانات را بر اساس CV به سه گروه تقسیم می کنیم.
جدول ۱- طبقه بندی نوسانات بر اساس ضریب تغییرات
توجه داشته باشید که معمولاً نوسانات اندک دارای مقادیر SCV است که به میزان قابل توجهی کمتر است از یک می باشد، در حالی که نوسانات بالا دارای SCV بالاتر از یک است. نوسانات متوسط نیز SCV نزدیک به یک دارد. برای مثال می خواهیم شاخص SCV یا مجذور ضریب تغییرات را برای شکل (۱) محاسبه کنیم. تمام داده هایی که داریم تنها نرخ تولید برای دو ایستگاه است که در ۵۰ درصد مواقع ۲ واحد و در ۵۰ درصد دیگر ۳ واحد می باشد.
برای بدست آوردن زمان تولید کافی است معکوس نرخ تولید را محاسبه کنید یعنی ۱/۲ و ۱/۳ که هر کدام را ضربدر احتمال وقوع که همان ۵۰ درصد یا ۱/۲ است کرده و با هم جمع می کنیم که در نهایت متوسط زمان فرآیند برای این خط تولید برابر ۰/۴۱۶= T می باشد. واریانس داده ها نیز برابر ۰/۰۰۶= σe۲ بدست می آید. نتیجه اینکه ۰/۰۴= SCV محاسبه می شود که معادل ۰/۲=CV است. عدد بدست آمده نشان می دهد نوسانات زمان تولید برای این خط ناچیز می باشد.
اثر تشکیل صف در خط تولید (Queuing Effects)
بدون تغییرات زیاد و نوسان داشتن، توضیح تئوری صف بسیار آسان می شود. اگر میزان نرخ بهره برداری از دستگاه ها زیر ۱۰۰ درصد باشد، زمان صف صفر خواهد بود. اگر میزان استفاده بالای ۱۰۰ درصد باشد، با رفتن زمان به بی نهایت، صف نامحدود می شود (بدون محدودیت). اما با حضور نوسانات، حتی زمانی که نرخ بهره برداری ماشین آلات کمتر از ۱۰۰ درصد است، میتوان یک صف ایجاد کرد.
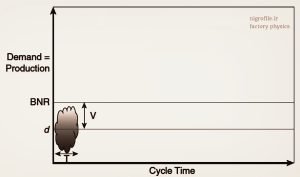
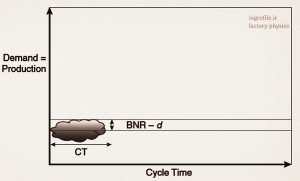
شکل (۲) یک خط تولید با نوسانات را نشان می دهد (که توسط فضای ابری نشان داده شده است). محور x نشان دهنده زمان سیکل تولید است و در این مثال، برابر است با زمان فرآیند T. محور y نشان دهنده تقاضا است، میانگین برابر با d و واریانس تقاضا با V نشان داده شده است. توجه داشته باشید که در بلندمدت میانگین تولید باید برابر با میانگین تقاضا باشد.
شکل ۴- یک سیستم تولیدی با حضور عوامل تصادفی و نوسانات
اگر تولید از تقاضا بیشتر شود، موجودی افزایش ادامه مییابد، در حالی که اگر تولید کمتر از تقاضا باشد، سفارشات معوقه بدون محدودیت رشد میکنند. در این مثال، نرخ گلوگاه (BNR) به طور قابل توجهی بالاتر از میانگین تقاضا تعیین می شود به طوری که تقاضا هرگز از ظرفیت فراتر نمی رود و هیچ صفی تشکیل نمی شود، بنابراین زمان سیکل تولید برابر با زمان فرآیند T است.
شکل (۳) نشان می دهد که با کاهش ظرفیت چه اتفاقی می افتد. از آنجایی که تولید نمی تواند از ظرفیت فراتر رود، فضای ابری مسطح می شود اما تا حدودی در حدود میانگین تقاضا متقارن باقی می ماند. از آنجایی که نوسان کاهش ظرفیت باید جایی اثر خود را نشان دهد، میتوان آن را در دل ظرفیت و نوسانات در زمان سیکل تولید نشان داد. این تفکیک دقیق نیست اما به نشان دادن این رفتار طبیعی کمک می کند.
شکل ۵- اثر نوسان کاهش ظرفیت در یک سیستم تولیدی
اگر مقدار نوسان ظرفیت ثابت بماند، مساحتی که با V × T نشان داده شده است باید برابر با CT (BNR – d) باشد. این یک روش شهودی برای تخمین زمان سیکل تولید (CT) ارائه می دهد:
![\[ V * T=CT (BNR-d)\]](https://nigrofile.ir/wp-content/ql-cache/quicklatex.com-27a890f78d8e6176f12f2bfd862e8650_l3.png "Rendered by QuickLaTeX.com")
![\[ =\frac{V * T} {BNR-d}\]](https://nigrofile.ir/wp-content/ql-cache/quicklatex.com-782ad6228cf84f81399f4ace97182c6d_l3.png "Rendered by QuickLaTeX.com")
![\[ CT=\frac{V * T^2}{1-u}\]](https://nigrofile.ir/wp-content/ql-cache/quicklatex.com-456ec339593ae6053efff9a94506018d_l3.png "Rendered by QuickLaTeX.com")
![\[ =\left(\frac{V }{d}\right) \frac{u}{1-u} T\]](https://nigrofile.ir/wp-content/ql-cache/quicklatex.com-fe82d5214a7efd7934bf9c764206aaee_l3.png "Rendered by QuickLaTeX.com")
![\[ =\text{VMR}\frac{u}{1-u} T\]](https://nigrofile.ir/wp-content/ql-cache/quicklatex.com-982ff4dc4383f1f69b551df71f18060e_l3.png "Rendered by QuickLaTeX.com")
که در رابطه بالا (VMR) نسبت واریانس به میانگین تمام تغییرات تعریف شده و برابر است با مجموع واریانس تقاضا و تولید تقسیم بر میانگین تقاضا (که میانگین تولید هم در نظر گرفته می شود). همچنین برای ایستگاه تولید تک ماشینی نرخ تولید گلوگاه برابر است با BNR = 1/T. این روابط یک تقریب نسبتاً خوب برای زمان سیکل تولید ارائه می دهد، به ویژه برای مقادیر نسبتاً بالای نرخ بهره برداری از ماشین آلات (u). با این حال،می توان یک تقریب بهتر هم نوشت که عبارت است از:
![\[ CT_{q}=\frac{VMR_{d}+SCV_{e}}{2}\frac{u}{1-u} T\]](https://nigrofile.ir/wp-content/ql-cache/quicklatex.com-53c90fdd59d13b0a53ed04cb76ad6b4d_l3.png "Rendered by QuickLaTeX.com")
که در آن CTq = میانگین زمان سیکل در صف، VMRd = نسبت واریانس به میانگین تقاضا، و SCVe = مجذور ضریب تغییرات زمان موثر فرآیند. در نتیجه کل زمان سیکل تولید به سادگی برابر خواهد با CT = CTq + T.
برای تولید به صورت دسته ای، زمان صف برای یک دسته باید محاسبه می شود. در این حالت، VMRd مربوط به ورود دسته ها است. به همین ترتیب، پارامترهای SCVe و T برای یک دسته هستند، نه برای یک واحد. رابطه بین مجذور ضریب تغییرات (SCV) برای تک قطعه با یک دسته از قطعات به صورت زیر است:
![\[ SCV_{Q}=\frac{SCV_{1}}{Q}\]](https://nigrofile.ir/wp-content/ql-cache/quicklatex.com-bbc17889261e4c71ab87a3493d177589_l3.png "Rendered by QuickLaTeX.com")
حالت ساده شده زمان سیکل تولید در هنگام تشکیل صف (CTq) به فرم زیر است که همان رابطه کینگمن می باشد که قبلاً معرفی کرده ایم:
![\[ CT_{q}=VUT\]](https://nigrofile.ir/wp-content/ql-cache/quicklatex.com-e1c1d9ad63870a8ff3081d7f318a3b4c_l3.png "Rendered by QuickLaTeX.com")
این معادله VUT داستان جالبی را بیان می کند. می گوید که زمان انتظار در صف برابر است با حاصلضرب یک ضریبی از نوسانات و عوامل تصادفی در یک ثابت بهره برداری یا استفاده از ماشین آلات (هر دو ضریب بدون بعد هستند) در میانگین زمان فرآیند. ضرایب ضرب می شوند نه جمع بنابراین معادله VUT نمایشی از مصالحه (tradeoff) بین زمان و ظرفیت است.
اگر مدیری بخواهد زمان سیکل تولید را پایین نگه دارد (یعنی CTq را پایین نگه دارد)، یا باید نوسانات را به حداقل رساند یا ضریب بهره برداری از ماشین آلات را پایین نگه دارد (این همان مفهوم مهم تولید بیش از اندازه هم یک اتلاف است که اوهنو در تویوتا به آن رسیده بود). ضریب بهره برداری کم نیز به معنی داشتن یک بافر ظرفیت بزرگ است.
یکی دیگر از کاربردهای جالب معادله VUT برای آن دسته از شرکتهایی است که داده های زمانسنجی مربوط به زمان فرآیند در ایستگاه های کاری و کل زمان سیکل تولید را ثبت می کنند. داشتن آن داده به این معنی است که شرکت اطلاعات CT و T را برای فرآیند خود دارد. در تعیین مکان بهبود و کوتاه کردن زمان سیکل تولید، یک مدیر می تواند از اطلاعات CT و T برای تعیین فاکتور VU برای بخش های مختلف یک کارخانه استفاده کند. مناطق با ارزش VU بالا معمولاً فرصتهای خوبی برای بهبود ارائه میدهند. یکی از مصادیق بهبود مستمر در همین نکته می باشد.
