محاسبات کاربردی در برنامه ریزی تولید
17
دی
برنامه ریزی تولید

محاسبات کاربردی در برنامه ریزی تولید

‫نوشته شده در تاریخ توسط گوبلای خان

بخش ششم : محاسبات کاربردی در برنامه ریزی تولید (Applied Calculations In Production Planning)

 

There are things which seem incredible to most men who have not studied Mathematics (Archimedes)

مفاهیمی وجود دارد که برای اغلب افرادیکه ریاضیات نخوانده اند غیر قابل باور است (ارشمیدس).

جهت یادآوری یکبار دیگر این باید بگوییم که ما در دنیای ایده آل که همه چیز از قبل مشخص است مانند این که بدانیم تقاضا برای محصولاتمان چقدر است و یا مواد اولیه مورد نیاز دقیقاً در زمانی که به آن نیاز داریم بدون هیچ تأخیری به دستمان می رسد و هیچ موجودی انبار نمی شود و غیره زندگی نمی کنیم. عدم قطعیت و نوسانات بخشی از زندگی روزمره ما می باشد و باید آنها را بشناسیم و در معادلات و تصمیم گیری ها در نظر بگیریم.

در ادامه مفاهیم مهم قبلی را با جزئیات بیشتری تشریح خواهیم کرد. اولین مفهوم محاسبات کاربردی در برنامه ریزی تولید زمان تکمیل یک سفارش مجدد برای مواد اولیه تا دریافت آن در انبار می باشد (Replenishment Time). تمام چیزی که نیاز دارید این است که اولاً بدانیم این نیاز چه زمانی احساس می شود مثلاً آیا نقطه سفارش تعریف کردیم یا خیر و دوم برای کالاهای مد نظر، زمان تکمیل فرآیند دریافت مواد را با واریانس و میانگین ثبت کنید.

به عنوان مثال، سیستم برنامه ریزی منابع سازمانی اوراکل  (Oracle ERP) سه جزء زمانی برای دریافت یک سفارش مواد تعریف کرده است: زمان های پیش پردازش (Preprocessing)، پردازش (Processing) و پس پردازش (post processing). زمان پردازش معادل زمان واقعی مورد نیاز برای تولید قطعه (در صورت ساخت داخل شرکت) یا خرید قطعه (از یک تامین کننده) است.

پیش پردازش شامل زمان تشخیص نیاز به سفارش خرید یا ساخت و صدور سفارش است. پس پردازش شامل زمان دریافت سفارش، بازرسی کیفی محصولات دریافتی، ثبت رسید و چیدمان داخل انبار است. سایر سیستم های ERP مشابه سیستم Oracle هستند، اما نام این فیلدها ممکن است کمی متفاوت باشد.

میانگین زمان تکمیل سفارش حاصل جمع این سه جزء و تقسیم بر تعداد آنها است. با این حال، این زمان ممکن است کمی پیچیده تر هم باشد مثلاً زمان تحویل فروشنده ممکن است با قوانینی در مورد مدت زمان ارسال پیش از موعد یا میزان تأخیر مجاز، ترکیب شود. به عنوان مثال، اگر به یک تأمین کننده اجازه داده شود که چهار روز زودتر اما بدون تأخیر اقلام را تحویل دهد، انتظار می رود زمان تکمیل سفارش برای این تأمین کننده کمتر از آنچه در سیستم ثبت شده است باشد.

همچنین، تأمین‌کننده‌ای که گاهی تأخیر می‌کند میانگین زمان تکمیل تا حدودی طولانی‌تر از آنچه در سیستم است، خواهد داشت. همه اینها می تواند موضوع را تا حد زیادی پیچیده کند اما برای یک تحلیل خوب زیاد به این جزئیات دقیق نیازی نداریم. به عنوان مثال، فرض کنید که اطلاعات زیر برای یک تأمین کننده در دسترس می باشد:

زمان پیش پردازش: ۳ روز
زمان پردازش: ۳۰ روز
زمان پس از پردازش: ۱ روز

همچنین تامین کننده مجاز به ارسال پنج روز زودتر و یک روز تاخیر است و این تامین کننده تقریباً در همین محدوده فعالیت می کند. پارامترهای زمان تکمیل سفارش عبارتند از:

میانگین زمان تکمیل سفارش= زمان پیش پردازش+ پردازش+ پس پردازش -(زمان ارسال زودتر/۲)+ (زمان ارسال با تأخیر/۲)

 میانگین = (۳+۳۰+۱)- (۲/۵)+ (۰/۵)=۳۲ روز

برای محاسبه واریانس (انحراف معیار) با فرض اینکه زمان بین ارسال زود و تأخیر دارای توزیع یکنواخت است خواهیم داشت:


    \[ =\sqrt\left( \frac{EARLY^2+LATE^2}{12} \right)\]

    \[=\sqrt\frac{5^2+1^2}{12}=1.5\]

نتیجه یک شاخص ارزیابی برای تأمین کننده ارائه می دهد. اگر در اغلب اوقات واریانس (انحراف معیار) زمان تحویل از دو روز بیشتر باشد نشان می دهد که این تأمین کننده قابل اعتماد نیست. اگر یک کالا دارای چند تأمین کننده مختلف باشد باز فرقی نمی کند هر کدام از تأمین کنندگان که از واریانس و میانگین مجموع این پیمانکاران، زمان کمتری داشته باشد دارای شاخص عملکرد بهتری است.

تقاضا (Demand)

مانند زمان تکمیل سفارش، واریانس و میانگین تقاضا هم باید مشخص شود. برای تقاضا فقط واریانس استفاده می شود و انحراف معیار موضوعیت ندارد. برای کنترل موجودی، میانگین و واریانس تقاضا در یک دوره معین مورد نیاز است. این دوره باید به اندازه ای طولانی در نظر گرفته باشد تا نتیجه قابل اتکاء داشته باشد. حداقل داده های ۱۰ دوره (روزانه، هفتگی، ماهیانه) را مد نظر داشته باشید.

تقاضای نشان داده شده در مثال جدول (۱) تقاضایی است که توزیع پوآسون را نشان می دهد. توزیع پوآسون توزیعی است که اگر تقاضا مربوط به بخشی از کل تقاضای یک جمعیت بزرگ باشد دیده می شود. فروش اینترنتی اغلب تقاضای پوآسون را نشان می دهد.

  جدول ۱- داده های مربوط به الگوی تقاضای پوآسن.

Random but Low-Variance Demand Pattern pic

برای این مثال میانگین و واریانس به ترتیب زیر محاسبه می شود:

    \[d= \frac{50.6}{5}=10.1\]

    \[\sigma_d^2=\frac{51.4}{5}=10.3\]

نسبت تقسیم واریانس به میانگین (variance-to-mean ratio) تقریباً دقیقاً ۱ است. این شاهدی است که توزیع این مثال در واقع یک توزیع پواسون است زیرا توزیع پواسون تنها یک پارامتر دارد که هم میانگین و هم واریانس برابر آن مقدار هستند. در نتیجه، همیشه نسبت واریانس به میانگین برای توزیع پواسون دقیقاً برابر ۱ است.

برای خواننده کنجکاو، این ممکن است عجیب به نظر برسد که چگونه یک توزیع می تواند یک پارامتر واحد هم برای میانگین و هم برای واریانس داشته باشد، با توجه به اینکه میانگین خطی است در حالی که واریانس مجذور است؟ تنها راهی که می‌تواند درست باشد این است که مدل‌ توزیع پواسون، متغیر تصادفی است که تنها یک عدد خالص بوده و هیچ بعدی ندارد.

به عبارت دیگر، توزیع پواسون نمی تواند یک متغیر تصادفی را برای فاصله، جرم، حجم، سرعت یا حتی نرخ تقاضا (Demand Rate) مدل کند. همه این مقادیر دارای بعد هستند به عنوان مثال، متر، کیلوگرم، لیتر و غیره. حتی نرخ تقاضا دارای بعد قطعه/ روز (یا دوره های دیگر) است. در حالی که قطعات به تنهایی هیچ بعدی ندارند.

در نتیجه، هنگام صحبت از تقاضا، تعداد واحدهای فروخته شده در یک دوره بدون مشخص کردن دوره بیان می شود. به این ترتیب تقاضا یک عدد خالص است. با این حال، ما اغلب در این مورد کمی ناپرهیزی می کنیم و در مورد تعداد واحدهای فروخته شده در روز یا هفته صحبت خواهیم کرد.

به عنوان مثالی دیگر تقاضا می تواند الگویی شبیه به آنچه در جدول (۲) درج شده، نمایش داده شود. دوره هایی با تقاضای صفر وجود دارد و پس از آن دوره هایی با تقاضای نسبتاً بالا وجود دارد. میانگین در این مورد ۲۷/۷ است و واریانس برابر ۸۹۹/۹ است، نسبت واریانس به میانگین برابر ۳۳ می باشد. این نمونه ای از تقاضای انبوه (Lumpy Demand) است و در بسیاری از زنجیره های تامین معمول است. این یکی از نشانه های تشخیص مفهومی است که به عنوان اثر شلاق چرمی (Bullwhip Effect) شناخته می شود.

این نوع تقاضا معمولاً برای تولید کننده های مانند باتری خودرو مشاهده شود. کل تقاضای مشتری برای باتری، همانطور که در فروشگاه‌های خرده‌فروشی دیده می‌شود، احتمالاً پواسون است، جایی که مشتریان هر بار یک باتری را خریداری می‌کنند. اما سفارش مجدد برای فروشگاه های خرده فروشی یک باتری در یک زمان نیست، بلکه یک حجم مشخصی باتری از یک عمده فروش یا خود کارخانه تولید کننده است.

     جدول ۲- داده های مربوط به الگوی تقاضای انبوه و اثر شلاق چرمی.  

Demand Example with Lumpy Demand pic

با انباشته شدن تقاضا در حجم زیاد، نوسانات افزایش می‌یابد، و عمده فروش تقاضایی را دریافت می کند که نسبت واریانس به میانگین بالاتری نسبت به ۱ دارد. در عین حال، خود عمده فروش هم سفارش حتی بزرگ‌تری به شرکت سازنده باتری‌ها می دهد. اثر این الگوی تقاضا این است که تولید کننده برای چندین هفته بدون تقاضا یا تقضای کم  و سپس با یک سفارش بزرگ روبرو خواهد شد که در نتیجه نوسان بسیار بالایی ایجاد می‌کند. این همان مفهوم اثر شلاق است یعنی نوسان کوچکی در منبع تقاضا باعث نوسانات شدید در انتهای زنجیره تأمین می شود.

خطای پیش بینی و زمان انتظار (Forecast Error and Lead Time)

اگر زمان تحویل کالا به مشتری از زمان تولید محصول بیشتر باشد در این حالت به ندرت به موجودی برای انبار کردن نیاز خواهیم داشت. زیرا تمام محصولات قبل از تاریخ سر رسید تحویل به مشتریان آماده شده اند. شاید تنها موردی که کالا را انبار خواهیم کرد در حالتی باشد که تولید بیشتر از تقاضا باشد یا مشتری بنا به دلائلی در خرید خود تجدید نظر کند.

با این حال، اگر زمان تحویل وعده داده شده به مشتریان کوتاه‌تر از زمان تولید باشد، ذخیره اطمینان محصولات همیشه باید در دسترس باشد همچنین تقاضای کالای نهایی باید پیش‌بینی شود و چنین پیش‌بینی‌هایی هم به دلیل اینکه خیلی وقت و انرژی برای بررسی مدل های مختلف صرف نمی شود، اغلب اوقات اشتباه است.

اگر تقاضا ثابت باشد، این پیش بینی می تواند صرفاً تخمینی از میانگین تقاضا باشد. در غیر این صورت، باید پیش‌بینی با هر روشی که در شرکت جاری است برای دوره‌های آتی محاسبه شود. هرچه پیش‌بینی‌ها بدتر باشد، موجودی بیشتری برای حفظ سطح خدمت به مشتری مورد نیاز خواهد بود.

اگر تقاضا ثابت باشد علاوه بر میانگین تقاضا، واریانس و محاسبه خطای پیش بینی هم مورد نیاز خواهد بود. خطای پیش بینی که در این جا بدان معرفی می شود عبارت است از میانگین مربعات خطا (Mean Square Error) که به اختصار (MSE) نامیده می شود و به شرح زیر محاسبه می شود:

    \[ MSE=\frac{\sum_{i=1}^{n}(D_i-F_i)^2} {n} \]

در معادله فوق:

D_i برابر تقاضای واقعی،

F_i پیش بینی برای دوره i می باشد.

اگر پیش بینی برای دریافت یک قطعه یا مواد از تأمین کننده باشد در اینصورت دوره پیش بینی معادل زمان انتظار دریافت کالا (Lead Time) خواهد بود. برای مثال اگر زمان دریافت یک کالا از تأمین کننده برابر ۶ هفته می باشد، دوره ی پیش بینی معادل همین ۶ هفته در نظر گرفته می شود.

نحوه پیش بینی هم به اینصورت است که در هفته اول i=1 برای ۶ هفته بعد پیش بینی می کنیم دوباره در هفته دوم هم برای ۶ هفته بعد پیش بینی انجام می شود و الی آخر. نتایج پیش بینی در هفته اول برای هفته دوم استفاده می شود و به همین صورت در مراحل بعدی این روش تکرار می شود. بعد از اینکه MSE  محاسبه شد در گام بعدی باید واریانس خطای پیش بینی را به صورت زیر محاسبه کنید:

    \[ \sigma_{d}^2=\frac{MSE} {n} \]

حالا از این مفاهیم چه استفاده ای می شود؟ در مرحله اول، اگر MSE را که محاسبه کرده اید از واریانس داده های تاریخی مربوط به تقاضا بزرگتر باشد این روش پیش بینی کاملاً گمراه کننده است و باید سراغ یک مدل دیگر بروید یا از خیر پیش بینی بگذرید و در این حالت از خود واریانس داده های تقاضا به عنوان معیاری برای تغییرات در تقاضا استفاده کنید.

در مرحله دوم، از آنجائیکه پیدا کردن مقدار بهینه برای MSE جهت پیش بینی به ویژه وقتی کالاها و دوره های زمانی زیاد باشد کاری وقت گیر است به جای این کار یک حد بالا برای واریانس داده های تقاضا مشخص می کنند. برای این منظور ابتدا نسبت واریانس به میانگین (Variance to Mean Ratio) را محاسبه می کنیم:

    \[ VMR=\frac {\sigma_d^2} {\lambda} \]

در ادامه فرض کنید که میانگین ۲۱۵ و واریانس ۱۲۰۳ برای تقاضای ۲۶ هفته گذشته یک محصول به دست آمده باشد. حال فرض کنید پیش بینی برای ۴ هفته آینده برابر ۲۵۰ واحد باشد. حد بالای واریانس داده های تقاضا برای دوره پیش بینی عبارت خواهد بود از:

    \[ \sigma_{F}^{2}=250*VMR=250*\frac{1203}{215}=1398.8 \]

معنی و مفهوم این عدد این که نشان دهنده حد بالای تغییرات در تقاضای داده های تقاضا می باشد این است که باید همواره MSE از این عدد کوچکتر باشد.

موجودی (Inventory)

در این قسمت برخی ملاحظات عملکردی راجع به کنترل موجودی ارائه می گردد. برای این منظور سیاست تعیین نقطه و مقدار سفارش مجدد (ROP/ROQ) در نظر گرفته شده است هر چند قابل تعمیم به سایر سیاست های کنترل موجودی هم می باشد. برای تنظیم نقطه سفارش مجدد دو پارامتر اصلی باید تعریف شود، مقدار سفارش مجدد (Reorder Quantity) و نقطه سفارش مجدد (Reorder Point) که هر زمان که موقعیت موجودی به نقطه سفارش یا پایین از آن رسید، تعداد/مقدار مشخصی کالا سفارش داده می شود. موقعیت موجودی (Inventory Position) به صورت تعریف می شود:

موقعیت موجودی= موجودی در دست (On Hand) + سفارش داده شده (On Order) – تعهدات معوقه (Backorder)

نقطه سفارش مجدد به صورت زیر تعریف می شود:

نقطه سفارش = متوسط تقاضا در زمان تأمین کالا (Average Replenishment-Time Demand) + ذخیره اطمینان (Safety Stock)

یا به اختصار:

r = λ ℓ + s

که در این رابطه (λ ℓ) معادل تقاضا در مدت زمان تأمین کالا و (S) برابر ذخیره اطمینان (احتیاطی) است. دقت کنید که برای محاسبه نقطه سفارش مجدد سطح خدمت را هم در نظر می گیرند یعنی این نقطه بدست آمده چند درصد تقاضا را پوشش می دهد. خلاصه هر موقع مقدار موجودی به این نقطه رسید، سیگنال تولید (خرید) صادر می گردد. اگر به دنبال ذخیره احتیاطی هستید با داشتن نقطه سفارش مجدد، می توانید به راحتی با استفاده از رابطه بالا ذخیره احتیاطی را محاسبه کنید، در ادامه مثالی آمده است. 

یک روش ساده برای اینکه بدانید سیاست کنترل موجودی که طراحی کرده اید درست است یا خیر این است که بدانید موقعیت موجودی (اغلب شامل موجودی در دست و سفارش داده شده)  باید همیشه بین  (ROP + 1) و (ROP + ROQ) باشد. در گام بعدی مهم است که بدانیم فرکانس (frequency) یا دفعات خرید یا ساخت کالای مد نظرمان چقدر است که روش محاسبه ساده ای دارد:

    \[f= \frac {D} {Q}\]

که در رابطه فوق (D) تقاضا و (Q) مقدار سفارش خرید یا ساخت است. اکر تعداد کل دفعات سفارش را برای چند کالا بخواهیم باید رابطه فوق را برای تک تک کالاهای مد نظرمان حساب کرده و با هم جمع کنیم.

    \[ \text {Average frequency}=\sum_{i}\frac{D_i} {Q_i} \]

برای مثال فرض کنید برای یک سیستم کنترل موجودی اطلاعات زیر را داشته باشیم:

نقطه سفارش مجدد برابر ۱۷ واحد،

مقدار سفارش برابر ۲۰ واحد،

متوسط زمان تأمین کالا ۶ روز و متوسط مصرف روزانه از این کالا ۲ واحد می باشد. مقدار ذخیره اطمینان برابر است با:

s = r − λℓ = ۱۷ − (۲ × ۶) = 5

البته یکی از معایبی که به روش (r,Q) وارد می باشد این است که خیلی به تقاضای آینده اهمیت نمی دهد یعنی اگر در آینده تقاضا صفر یا دو برابر شود این اعداد ثابت هستند. اگر در شرکت خود تقاضاهای آینده معلوم یا بر اساس پیش بینی فعالیت می کنید می توانید از رویکرد دیگر که (Time-phased reorder policies) نام دارد استفاده کنید.

در این روش پس از تعیین ذخیره احتیاطی، هر زمانیکه موقعیت موجودی به کمتر از ذخیره احتیاطی رسید، سیگنالی جهت سفارش مجدد صادر می کند و برای مقدار سفارش، اول مشخص می کنیم چقدر از ذخیره اطمینان کم داریم، دوم تقاضای چند دوره جلوتر که مد نظرمان است را حساب کرده به عدد قبلی اضافه می کنیم و عدد نهایی را به عنوان مقدار سفارش در نظر می گیریم.

برای مثال فرض کنید برای محصولی ذخیره اطمینانی برابر ۱۰۰ واحد در نظر گرفتیم. بعد از کنترل های انجام شده، موقعیت موجودی عدد ۹۸ را نشان می دهد و یک سیگنال جهت خرید با تولید مجدد صادر می کند. در اینجا سیاست شرکت این است که تقاضای ۵ دوره آتی را حساب کرده (در اصطلاح Days Of Supply -DOS) و مثلاً برابر ۵+۰+۱+۲+۵= 13 واحد کالا شده است.

در ادمه ۲ واحد کالا تا تکمیل ذخیره احتیاطی داریم بعلاوه ۱۳ واحد تقاضای آینده، می شود ۱۵ واحد که یا باید بخریم یا خودمان تولید کنیم. بدیهی است که اگر قرار باشد این محصول را خریداری کنیم و فروشنده کمتر از ۲۵ واحد نمی فروشد باید همین ۲۵ واحد را سفارش دهیم.

نکته مهم بعدی این است که میانگین موجودی یک معیار مهم است، اما باید همراه با نرخ استفاده از موجودی در نظر گرفته شود. به عنوان مثال، داشتن ۱۰۰۰ قطعه موجودی از یک کالایی ممکن است زیاد به نظر برسد، اما اگر ۱۰۰۰ قطعه در هفته مصرف شود، داشتن ۱۰۰۰ قطعه در دسترس به معنای داشتن موجودی فقط برای مصرف یک هفته است. به همین دلیل است که معیار متفاوتی به نام گردش موجودی ( Inventory turns) مورد استفاده قرار می گیرد و به صورت زیر تعریف می شود:

    \[ \text{Inventory Turns}=\frac {\text{COGS value of annual sales}} {\text {COGS value of on hand}} \]

که صورت کسر معادل ارزش پولی کالای فروخته شده در یک سال و مخرج کسر نیز برابر ارزش پولی موجودی فعلی (در دسترس) می باشد. توجه داشته باشید که گردش موجودی، مانند بسیاری از نسبت‌های مالی، یک نسبت بدون بعد (dimension) نیست. بلکه گردش موجودی دارای بعد ۱ / سال است. بنابراین میانگین روزهای فروش محصولات برابر خواهد بود با:

    \[ \text{Average days to sell inventory}=\frac {365} {\text {Inventory turns}} \]

در مخرج کسر نتیجه رابطه گردش موجودی درج می شود. می توانید برای محاسبات کنترل موجودی محصولات خود شامل نقطه سفارش، مقدار سفارش، ذخیره احتیاطی و حداکثر موجودی بدون زحمت و در عین حال داشتن نتایج قابل اتکاء از نرم افزار و دستیار تخصصی کنترل موجودی استفاده نمایید. برای کسب اطلاعات بیشتر می توانید اینجا کلیک کنید.

تخمین نرخ تکمیل سفارشات (Estimating Fill Rate)

نرخ تکمیل سفارش مشتری کسری از زمانی است که سفارشات و تعهدات معوقه نداریم. نوسانات ناشی از تصادفی بودن تقاضا و زمان دریافت مواد از تأمین کننده، عوامل اصلی دشوار بودن محاسبات این بخش محسوب می گردد. همانطور که قبلاً بحث شد یک عامل کلیدی، میزان تقاضا در زمان تأمین کالا  (replenishment-time demand) است و در واقع یک متغیر تصادفی (Random Variable) بوده و نشان دهنده تقاضای تصادفی در بازه زمانی دریافت کالا است که خود این زمان تأمین هم تصادفی می باشد. واریانس و میانگین این متغیر تصادفی به ترتیب عبارت است از:

    \[\mu_{RTD}=\lambda \ell\]

    \[\sigma_{RTD}^2=\ell\sigma_{d}^2+\lambda^2\sigma_{\ell}^2\]

اگر X نشان دهنده متغیر تصادفی تقاضا در بازه زمانی تحویل سفارش کالا به انبار باشد، احتمال اینکه در یک موقعیت موجودی خاصی ما کالای مورد نظر را در انبار نداشته باشیم (stock out) عبارت است از:

Pr{stock-out with IP = x} = Pr{X > x} = 1 − F(x)

که در آن F(x) تابع توزیع تجمعی تقاضای زمان تأمین است. از آنجائیکه موقعیت موجودی برای یک سیستم نقطه سفارش همیشه بین r + 1 و r + Q است، مقادیر Q متفاوتی را به دست می دهد، می توانیم با میانگین گیری در این بازه، میانگین نرخ تکمیل سفارشات مشتری را با تکیه بر سیستم کنترل موجودی که طراحی کردیم تخمین بزنیم:

    \[\bar{S}=\frac{1}{Q} \sum_{x=r+1}^{r+Q} Pr \{ X\leqslant x \}= \frac{1}{Q} \sum_{x=r+1}^{r+Q} F(x)\]

در ادامه همان مثال بالا را که ذخیره اطمنان را حساب کردیم یک بار دیگر را در نظر بگیرید ولی این بار فرض کنید ذخیره اطمینان صفر باشد. همچنین باید اطلاعاتی در مورد واریانس تقاضا و زمان تکمیل فرآیند تأمین داشته باشیم، بنابراین فرض کنید تقاضا پواسون است (به این معنی که واریانس تقاضا با میانگین که مقدار ۲ دارد برابر است) و انحراف استاندارد زمان تأمین کالا نیز ۱ روز است. با این داده های جدید ROP برابر است با:

    \[\text{r}=\lambda\ell+s=2*6+0=12\]

در نتیجه:

    \[\mu_{RTD}=\lambda \ell=2*6=12\]

    \[\sigma_{RTD}^2=\ell\sigma_{d}^2+d^2\sigma_{\ell}^2=6*2+2^2*1=16\]

    \[\sigma_{RTD}=4\]

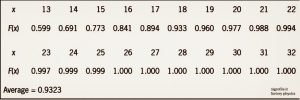
انحراف استاندارد ۴ به طور قابل توجهی کوچکتر از میانگین (۱۲) است لذا می توان از توزیع نرمال استفاده کرد. با مقدار سفارش ثابت برابر ۲۰ واحد و با استفاده از اکسل می توانیم جدول احتمالات را برای هر مقدار ممکن از موقعیت موجودی محاسبه کنیم. نتایج در جدول (۱) درج شده است.

جدول ۱- نتایج احتمالات

Table of Probabilities pic

برای مثال x برابر ۱۳ همان R+1 یعنی ۱۲+۱ می باشد برای محاسبه احتمال از تابع توزیع نرمال NORMDIST(13,12,4,TRUE) در اکسل استفاده شده است که نتیجه ۰/۵۹۹ را بر می گرداند. در این تابع عدد ۱۲ همان میانگین، عدد ۴ برابر انحراف معیار و مقدار توزیع تجمعی در حالت TRUE قرار می گیرد. میانگین مورد انتظار نرخ تکمیل سفارش مشتری برای این مثال برابر ۰/۹۳ درصد می باشد. توجه داشته باشید که این احتمال با فرض این است که سیستم، سفارشات معوقه ندارد. به بیان دیگر این درصد تکمیل سفارشات از موجودی انبار می باشد.

دو نکته مهم:

الف: اگر انحراف معیار کوچکتر از میانگین باشد (حدود یک سوم میانگین) توزیع نرمال به ترتیبی که در مثال بالا ذکر شده به خوبی جواب می دهد. در غیر اینصورت از این توزیع استفاده نکنید.

ب: می توان برای نرخ تکمیل سفارش مشتری یا به تعبیری سطح خدمت، یک حد پایین (Lower Bound) تعریف کرد. برای مثال بالا این مقدار برابر است با:

    \[\bar{S}_{LB}=\frac{F(r+1)+F(r+Q)}{2}=0.80\]

نتیجه اینکه با توجه با داده های مثال گفته شده برای یک سیستم کنترل موجودی، متوسط سطح خدمت به مشتریان ۰/۹۳ درصد و حداقل آن برابر ۰/۸۰ درصد خواهد بود.

سیاست های محاسباتی موجودی (Computing Inventory Policies)

هنگام تنظیم سیاست های کنترل موجودی، باید سه هدف را در نظر بگیریم:

۱. مقدار پول سرمایه گذاری شده در موجودی حداقل باشد.
۲. سطح خدمات به مشتری حداکثر باشد.
۳. تعداد دفعات سفارش خرید یا ساخت نیز در حداقل قرار گیرد.

همانطور که ملاحظه می گردد این اهداف در تضاد با یکدیگر هستند و تنها راهی که بتوان همزمان هر سه مورد را مد نظر قرار داد استفاده از نمودار مرز کارآیی (Efficient Frontier) است که قبلاً به آن اشاره کرده ایم. راه هایی از جمله دادن ضرائب یا وزن و سعی در بهینه کردن آنها خیلی شهودی نمی باشد از طرفی پیدا کردن وزن یا ضریب مناسب هم مشکل است. مرز کارایی برای تعداد دفعات سفارش دهی متفاوت به دست می آید و هر مرز حداقل سرمایه  مورد نیاز موجودی را برای یک نرخ تکمیل سفارش مشخص، نشان می دهد.

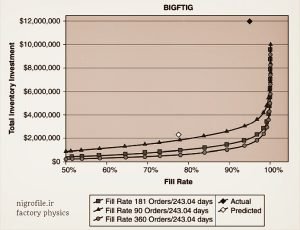
شکل (۱) منحنی‌های مرزی کارایی را برای یک تولیدکننده لوله و اتصالات نشان می‌دهد که از سیستم کنترل موجودی استفاده نکرده و فقط بر حسب تجربه یا آزمون و خطا جلو رفته است. سه منحنی وجود دارد که هر یک نشان دهنده تعداد متفاوت سفارش دهی در سال می باشد. ۳۶۰ بار سفارش در سال، ۱۸۱ سفارش در سال و نهایتاً ۹۰ سفارش در سال است. همانطور که ملاحظه می گردد کمترین تعداد سفارش دهی در سال که مربوط به ۹۰ است بالاترین نرخ سرمایه گذاری را دارد.

Efficient frontiers for inventory pic

  شکل ۱- مرز کارآیی برای موجودی (برای بزرگنمایی روی تصویر کلیک کنید)

در نرخ تکمیل سفارشات کمتر از ۹۸ درصد، با افزایش تعداد دفعات سفارش دهی از ۸۰ به ۱۸۱، کاهش سرمایه گذاری در موجودی همراه با حفظ سطح خدمت مشاهده می گردد اما با افزایش از ۱۸۱ به ۳۶۰ بهبود ناچیزی مشاهده می شود. دلیل آن این است که اولاً از یک طرف با افزایش تعداد دفعات خرید، حجم خرید هم کمتر خواهد شد لذا متوسط موجودی کاهش خواهد یافت لذا منابع پولی کمتری درگیر موجودی می شود.

اما از طرف دیگر اگر تعداد دفعات خرید را خیلی بالا ببریم (۳۶۰ سفارش) ممکن است به دلیل نبود کالا در انبار به تعداد کافی، سطح خدمت به مشتری آسیب ببیند در این حالت نیاز به دخیره اطمینان ضروری می شود. در تعداد سفارش ۱۸۱ بار در سال، خیلی به موجودی اطمینان نیاز نداریم و اثر منفعت حاصل از کاهش سرمایه گذاری در موجودی محسوس است اما وقتی تعداد سفارش دهی زیادتر شود کاهش سرمایه گذاری در موجودی با نیاز به افزایش ذخیره اطمینان خنثی می شود.

این مفهوم بسیار خوبی برای افزایش شهود است که افزایش تعداد سفارش دهی از یک تعدادی به بعد باعث کاهش در موجودی نخواهد شد. در مرحله بعد خود افزایش در تعداد سفارش خرید یا ساخت هم به عنوان یک منبع ایجاد نوسان شناخته می شود که اثر منفی دارد. نمودار همچنین دو نقطه خاص را نشان می دهد: یک الماس سفید که عملکرد مورد انتظار را با استفاده از پارامترهای داده شده نشان می دهد و یک الماس سیاه که عملکرد فعلی سیستم را نشان می دهد. در یک سیستمی که خوب طراحی شده، اینها نزدیک خواهند بود اما در این مثال آنها از هم دور هستند چرا؟

به نظر می رسد که سیاست های موجود شرکت برای بالا نگه داشتن سطح خدمت از نظر آنها کافی نبوده است. برنامه ریزان می دانند که تمام شدن موجودی بدتر از داشتن موجودی زیاد است، بنابراین سیاست ها را نادیده می گیرند و از شهود خود استفاده می کنند. این دو الماس با ۱۸۱ سفارش در سال بر هم منطبق می شوند. در نتیجه می‌توانیم موجودی را از ۱۲ میلیون دلار به حدود ۳ میلیون دلار با افزایش قابل توجهی در سطح خدمت به مشتری کاهش دهیم.

ملاحظات کنترل موجودی در مونتاژ (Inventory in an Assembly System)

سیستم‌های تولیدی که بر اساس سفارش اقدام به تولید محصول می کنند (Make To Order) می‌توانند به لحاظ کاهش موجودی و ارائه خدمات بالا به مشتریان سودمند باشند. ملاحظاتی باید در مورد طراحی لجستیکی یک سیستم تولید و مونتاژ سفارشی در نظر داشت شامل:

الف: برای اینکه بتوانیم بر حسب تقاضا مونتاژ کنیم، به مقدار زیادی موجودی نیاز داریم، چرا که باید قطعات و مواد لازم را در زمان تولید محصول مورد تقاضا داشته باشیم. اما بحثی که وجود دارد این است که مصالحه (Tradeoff) بین مونتاژ برحسب تقاضا (Assemble on Demand)، مونتاژ برمبنای سفارش (Assemble To Order) و اصولاً بین خرید یا ساخت چیست؟

ب: معیار خدمات مناسب به مشتری چیست؟ نرخ تکمیل سفارش، تعداد سفارشات معوقه، میزان تأخیر در ارسال سفارش ؟ چگونه این موارد با آنچه معمولاً استفاده می شود مقایسه می شود؟

جذابیت مونتاژ بر مبنای سفارش را می توان از منظر استفاده بهتر از بافرها به ویژه زمان و موجودی توضیح داد. در مونتاژ بر مبنای سفارش، می توان به منظور کاهش موجودی، از بافر زمان استفاده کرد یعنی در این سیستم می توانیم پس از دریافت سفارش، مواد و قطعات گران قیمتی که نمی شود آنرا انبار کرد را تهیه کرده و پس از آماده شدن محصول به مشتری تحویل داد. در این سیستم اگر هم تأخیری بابت جفت وجور کردن قطعات داشته باشیم خیلی مشتری را اذیت نمی کند چراکه این روش برای آن دسته از کالاهایی است که مشتری معمولی برای آنها وارد فروشگاه نمی شود و فوراً آن را مطالبه نمی کند.

برای مثال یک محصول را در نظر بگیرید که به شش جزء نیاز دارد، و سه گزینه برای هر جزء وجود دارد که در مجموع ۷۲۹=۶^۳ پیکربندی ممکن را ارائه می دهد. فرض کنید هر جزء ۱۵۰ واحد پولی هزینه دارد، بنابراین هر پیکربندی ۱۹۰۰=۱۵۰*۶ واحد پولی هزینه خواهد داشت. فرض کنید که تقاضای برای هر پیکربندی مساوی و برابر  ۱۰۰ واحد در سال باشد و همچنین قطعات از یک تامین کننده خارجی با زمان تحویل ۹۰ روزه تهیه می شود.

اگر فقط از یک بافر زمانی برای متعادل کردن تقاضا و تولید استفاده شود، مشتری باید حداقل ۹۰ روز صبر کند تا مواد برسد. تازه مقداری زمان هم باید برای انجام مونتاژ به این زمان اضافه شود. اما اگر بخواهیم همه ۷۲۹ طراحی ممکن از محصول را تولید و انبار کنیم مبلغی حدود ۱۱۷۰۰ واحد پولی برای هر پیکربندی باید هزینه شود تا به سطح خدمت ۹۹ درصدی برسیم که سرجمع حدوداً ۸۵۲۹۰۰۰ واحد پولی سرمایه نیاز خواهد داشت.

راه حل دیگر استفاده از روش مونتاژ بر مبنای سفارش است. در این حالت، مشتری فقط مدت کوتاهی برای مونتاژ منتظر می ماند و به جای ۷۲۹ پیکربندی مختلف، تنها ۱۸ جزء مختلف باید ذخیره شود. برای به حداقل رساندن موجودی، زمان تحویل هر جزء یکسان فرض شده است که برابر خواهد بود:

    \[0.99^{1/6}=0.9983\]

سرمایه‌گذاری مورد نیاز برای انجام این کار ۶۲۴۰۰۰ واحد پولی است که ۹۳ درصد کمتر از تولید و انبارکردن تمام ۷۲۹ کالای نهایی است. بنابراین عملیات مونتاژ بر مبنای سفارش با استفاده مناسب از هر دو بافر زمان و موجودی باعث کاهش منطقی هزینه خواهد شد.

مدلسازی جریان تولید (MODELING FLOW)

جریان جایی است که عملیات تولید انجام می شود. در یک جریان، مواد خام به محصولی که مشتری نیاز دارد و حاضر است برای آن پول پرداخت کند تبدیل می شود. جریان مجموعه ای از مسیرهای تولید است. هر مسیر (routing) مقدار مشخصی از مواد را از یک انبار تحویل می گیرد و آن را از طریق مجموعه ای از حداقل یک مرحله پردازش به نقطه انبار دیگری تحویل می دهد. در مباحث گذشته نمودار عملکرد، قانون لیتل و معادله کینگمن (VUT) معرفی شدند. اکنون می خواهیم ببینیم که برخی از این روابط از کجا سرچشمه می گیرند.

قانون لیتل (Little’s Law)

سه معیار مهم برای هر خط تولید عبارت است از: نرخ تولید (Throughput, or TH)، مقدار کار در حال انجام روی خط (WIP) و مدت زمانی که طول می کشد تا محصول از خط تولید عبور کند (Cycle Time, or CT). این سه معیار اصلی در واقع ۳ بافر مهم برای متعادل سازی بین عرضه و تقاضا هستند. به عبارت دیگر وقتی که تقاضا برای محصول شما از توان تولیدتان بالاتر باشد معمولاً یکی از گزینه های زیر را انتخاب می کنید:

الف) اگر محصول سفارشی است می توانید برخی از اجزاء و قطعات گران قیمت را بعد از دریافت سفارش و با گرفتن پیش پرداخت از مشتری تهیه نمایید. در این حالت ممکن است زمان سیکل تولید کمی افزایش یابد ولی از آنجائیکه مشتری برای محصول سفارشی صبر و حوصله بیشتری دارد قابل توجیه است. با انتخاب این گزینه شما از بافر زمان (طولانی کردن زمان سیکل تولید) برای همسان سازی استفاده می کنید.

ب) برای برخی از محصولات که سفارشی نیستند و اگر به هر دلیل شما نتوانید تقاضا را پوشش دهید مشتری به سراغ فروشنده دیگر می رود، می توانید موجودی بیشتری در انبار نگهداری کنید تا در مواقع افزایش تقاضا بتوانید جوابگو باشید. با اتخاذ این سیاست شما از بافر موجودی در مقابل نوسان تقاضا استفاده می کنید.

ج) در حالتی که با افزایش موجودی باز هم جوابگوی تقاضا نباشید باید سراغ افزایش ظرفیت بروید که شامل طیفی از اقدامات از جمله اضافه کاری، برون سپاری، استخدام و در نهایت اضافه کردن ماشین آلات یا حتی خطوط جدید تولید است. این راه حل گرانترین است اما در برخی مواقع باید سراغ این گزینه بروید که همان بافر ظرفیت است.

شاید در شرکت محل فعالیت خودتان راه حل های دیگری هم استفاده کنید اما این سه بافر به عنوان اقدامات اصلی شناخته می شوند. نکته مهم  این است که این سه ابزار مهم با هم در ارتباط هستند و اگر بدون شناخت این مفهوم برای هر کدام جداگانه برنامه ریزی کنید ممکن است اثر منفی بر دو گزینه دیگر داشته باشد. برای مثال اگر تحت عنوان موجودی صفر، شروع به کاستن از موجودی کنید ممکن است به توان عملیاتی آسیب بزنید و زمان سیکل تولید افزایش یابد و مشتریان با افزایش زمان انتظار دریافت محصول ناراضی شوند.

مفهومی که این ارتباط را توضیح می دهد قانون لیتل نام دارد (برای توضیحات بیشتر به بخش مربوط به دنیای یک متخصص برنامه ریزی تولید مراجعه کنید). این قانون هم مبنای تجربی دارد و هم ریاضی و برای مهندسین تولید کارکردی شبیه قانون معروف دوم نیوتن (F= m.a) دارد که برای مهندسی مکانیک اساسی است. برای درک بهتر این قانون مثال شکل (۲) را در نظر بگیرید که WIP را در یک سیستم تک ماشینی به عنوان تابعی از زمان و با چهار نوع کار/قطعه متفاوت نشان می دهد.

کارهای مورد نیاز، زمان‌های فرآیند متفاوتی دارند، A و B به چهار ساعت نیاز دارند، C به سه ساعت در حالی که تکمیل D به پنج ساعت زمان نیاز دارد. در مدت زمان بررسی ۲۰ ساعته، کار A در ساعت دوم می رسد، B در ساعت ۳، C در ساعت ۵ و در نهایت، D در ساعت ۱۵ می رسد. میانگین (TH)، (WIP) و (CT) در طول ۲۰ ساعت چگونه محاسبه می شود؟

Illustration of Little’s law pic

  شکل ۲- مثالی از قانون لیتل

میانگین نرخ تولید یا توان عملیاتی (TH) آسان است: ۴ کار در ۲۰ ساعت. TH = 4/20 = 0/2 کار در ساعت. برای زمان سیکل تولید (CT)  زمان فرآیند و مدت زمان انتظار قطعه را باید با هم در نظر بگیریم لذا این زمان برای قطعه یا کار (A) برابر ۴ ساعت، کار (B) 7ساعت، کار (C) 8 ساعت، و در نهایت کار (D) 5 ساعت. میانگین زمان هر قطعه در سیستم برابر است با ۶=۲۴/۴ ساعت.

محاسبه کار در جریان تولید هم آسان است به سادگی تعداد WIP را در هر دوره جمع کنید و بر زمان دوره تقسیم کنید. توجه به این نکته مهم است که مجموع WIP در هر دوره برابر است با مجموع زمان سیکل. دقت کنید برای زمان‌های سیکل، از چپ به راست می‌شماریم، و برای WIP، از پایین به بالا می‌شماریم، اما مجموع یکسان و برابر ۲۴ خواهد بود. بنابراین میانگین ۲۴/۲۰ = 1/۲ می باشد. راه دیگر محاسبه کار در جریان ساخت با استفاده از دو میانگین توان عملیاتی و زمان سیکل است یعنی:

WIP = TH × CT

۶ * ۰/۲ =۱/۲

که به قانون لیتل معروف است. توجه داشته باشید در این مثال فرض گرفتیم در قبل از این دوره ۲۰ ساعته ماشین بیکار بوده است. این ساده سازی به نتیجه کلی لطمه نمی زند و نشان دادیم که قانون لیتل یک قانون کاملاً تجربی است. اگر زمان دوره بررسی را طولانی تر در نظر بگیرید حتی با وجود کار در جریان ساخت قبل از ثبت زمان شبیه سازی، نتیجه خیلی تفاوتی نمی کند.

تعریف گردش موجودی، کاربردی دیگر از قانون لیتل است. اگر از کار در جریان ساخت به عنوان نماینده موجودی استفاده کنیم (اگرچه WIP به طور دقیق یک معادل موجودی نیست) و از توان عملیاتی برای نشان دادن بازده فروش آنگاه خواهیم داشت:

    \[ \frac{TH}{WIP}=\frac{1}{CT} \]

طبق نتیجه بدست آمده، گردش موجودی برابر معکوس زمان سیکل تولید می باشد. بنابراین دارای بعد (dimension) زمان/ ۱ خواهد بود.

گوبلای خان

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

error: Content is protected !!