برنامه ریزی ادغامی
26
خرداد
برنامه ریزی تولید

برنامه ریزی ادغامی

‫نوشته شده در تاریخ توسط گوبلای خان

بخش پانزدهم؛ برنامه ریزی ادغامی (Aggregate Planning)

برنامه ریزی ادغامی یک فعالیت عملیاتی مهم برای یک شرکت تولیدی است زیرا به دنبال تعادل بین تصمیمات بلند مدت با موفقیت تولید در کوتاه مدت است.

برخی از تصمیمات مدیریتی نیاز به دانستن برنامه های تولید برای یکسال آینده یا حتی فراتر از آن دارد از جمله :

الف) منابع انسانی (Staffing)؛ استخدام و آموزش پرسنل جدید فرآیندی زمان بر است. مدیریت به یک برنامه تولید بلندمدت نیاز دارد تا تصمیم بگیرد چه تعداد و از چه تخصص هایی باید استخدام کند. و یا برعکس، تعدیل کارگران پرهزینه و دردناک می باشد، اما گاهی ضروری است. پیش‌بینی کاهش تولید از طریق یک برنامه بلندمدت، استفاده از رویکردهای ملایم‌تر را برای دستیابی به حداقل بخشی از تعدیل پرسنل ممکن می‌سازد.

ب) تأمین و تدارکات (Procurement)؛ قبل از ثبت سفارشات با پیمانکاران اغلب نیاز به عقد قرارداد است. فرآیند شناسایی و تأیید صلاحیت تأمین کنندگان نیاز به زمان دارد. علاوه برآن، خرید برخی از قطعات طولانی می باشد (مثلاً برای قطعات با فناوری پیشرفته ممکن است به ۶ ماه یا بیشتر نیاز باشد). بنابراین تصمیم گیری در مورد قراردادها و سفارشات باید بر اساس یک برنامه تولید بلندمدت اتخاذ شود.

ج) برون سپاری (Outsourcing/Subcontracting)؛ گاهی نیاز است قراردادهایی با پیمانکاران فرعی برای ساخت برخی قطعات یا انجام عملیات خاص قبل از ارسال سفارشات منعقد شود. تعیین اینکه از چه نوع پیمانکاری فرعی استفاده شود، نیازمند پیش بینی های بلندمدت تولید و اصلاح ظرفیت است.

د) بازاریابی (Marketing)؛ پرسنل واحد بازاریابی و فروش باید بر اساس پیش‌بینی تقاضا و آگاهی از اینکه کدام محصول ظرفیت تولید محدودی دارد و کدام محصول نه، تصمیم بگیرند که روی کدام محصولات مانور بیشتری داشته باشند. برای این منظور یک برنامه تولید بلندمدت مورد نیاز است.

همانطور که ملاحظه می کنید به این دلیل که بسیاری از تصمیمات مدیریتی به برنامه تولید آینده بستگی دارد، بسیاری از فرمول بندی های مختلف نیز امکان پذیر است. اینکه کدام فرمول مناسب است بستگی به تصمیمی دارد که در کانون توجه قرار می گیرد.

 یک مدل برای تعیین نیازمندی های منابع انسانی ممکن است با مدلی برای تصمیم گیری اینکه کدام محصول یا قطعات باید توسط پیمانکاران فرعی تولید شوند بسیار متفاوت باشد. حتی اگر بخواهیم هر دو موضوع را به طور همزمان بررسی کنیم، ممکن است بررسی یک مدل متفاوت منطقی باشد.

برنامه‌ریزی خطی (Linear Programming) ابزار مفیدی برای فرمول‌بندی و حل بسیاری از مسائلی است که معمولاً در برنامه‌ریزی تولید ادغامی با آن مواجه می‌شویم. در این بخش دو مسئله معمولی برنامه ریزی تولید ادغامی را به عنوان مسائل خطی فرموله و حل می کنیم.

هدف ما ارائه راه حل برای برنامه های ادغامی خاصی نیست، بلکه بیشتر نشان دادن رویکردهای کلی حل مسئله است. با توجه به نکات گفته شده در اینجا و اندکی تلاش می تواند مسئله مورد نظر خودتان را فرمول بندی، حل و تفسیر نمایید.

پیش فرض مطالب ارائه شده این است که خواننده محترم با مفاهیم اولیه و پایه ای برنامه ریزی خطی آشنایی دارد. اگر اینطور نیست قبل از ادامه بحث یه مرور هرچند مختصر داشته باشید.

بحث را با برنامه‌ریزی تولید ادغامی ساده شروع می‌کنیم. در مثال های ارائه شده فرض می شود که پیش‌بینی تقاضا انجام شده یا تقاضای هر دوره در افق برنامه‌ریزی مشخص است. دوره های برنامه ریزی معمولاً ماهانه است. اما افق برنامه ریزی تولید ادغامی بین یک تا سه سال می باشد.

مدل ساده برنامه ریزی تولید ادغامی (Simple Model)

سناریوی اول ما ساده ترین حالت ممکن را نشان می‌دهد دلیل آن هم این است که در یک نمای کلی، مسائل اساسی را نشان می‌دهد و مبنایی برای در نظر گرفتن شرایط واقعی‌تر فراهم می‌کند همچنین نشان می‌دهد که چگونه برنامه‌ریزی خطی می‌تواند از برنامه‌ریزی ادغامی پشتیبانی کند.

در یک مدل ساده، وضعیتی را در نظر می‌گیریم که تنها یک محصول وجود دارد. در هر دوره، پیش‌بینی تقاضا انجام شده و محدودیت ظرفیت هم داریم. برای سادگی فرض شده که تقاضا معادل سفارشات‌ مشتری است و در پایان دوره تحویل می گردد. نوسانات و تصادفی بودن متغیرها که منجر به فروش از دست رفته خواهد شد، در نظر گرفته نمی شود.

با این مفروضات بدیهی است که اگر تقاضا در هر دوره کمتر از ظرفیت باشد، راه‌حل بهینه تولید مقادیری برابر با تقاضای هر دوره است. با این کار تمام تقاضا به موقع برآورده می شود و بنابراین هیچ موجودی اضافه ای بین دوره ها ایجاد نمی کند. با این حال اگر تقاضا در برخی دوره‌ها از ظرفیت تولید فراتر رود، باید جلوتر تولید کنیم (تولید بیش از نیازمان در دوره‌های قبلی). اگر حتی با روش هم نشود تقاضا را برآورده کرد، ما می خواهیم مدل ما این را به ما بگوید. برای مدل سازی این وضعیت در قالب یک برنامه خطی، نمادهای زیر معرفی می گردد:

t = شاخصی از دوره های زمانی، که در آن t =1 . . .  ، ṫ می باشد. بنابراین ṫ معادل افق برنامه ریزی است.

 dt = تقاضا در دوره t

ct = ظرفیت در دوره t

r = سود دریافتی به ازای هر واحد محصول فروخته شده (بدون احتساب هزینه نگهداری موجودی).

h = هزینه نگهداری یک واحد موجودی برای یک دوره

Xt = مقدار تولید شده در دوره t (فرض می شود برای برآوردن تقاضا در پایان دوره t موجود است).

 St = مقدار فروخته شده در دوره t (فرض می کنیم که واحدهای تولید شده در t برای فروش در t و پس از آن در دسترس هستند).

I۰ = موجودی در پایان دوره t بعد از برآورده شدن تقاضا (فرض می شود I۰ به عنوان داده ورودی به مسئله مشخص است).

در این مدل، Xt، St و It متغیرهای تصمیم (Decision Variables) هستند. یعنی برنامه کامپیوتری که LP را حل می کند آزاد است که مقادیر این متغیرها را طوری انتخاب کند که علاوه بر تابع هدف، محدودیت ها نیز برآورده شوند.

سایر متغیرها شامل dt , ct , r , h مقادیر ثابت هستند که باید برای سیستم واقعی تخمین زده شوند و به عنوان اطلاعات اولیه مسئله ارائه شوند. برای متغیرهای تصمیم از حروف بزرگ و ثابت های مدل از حروف کوچک استفاده می شود.

ما می توانیم مدل به حداکثر رساندن سود منهای هزینه حمل موجودی را با توجه به محدودیت های ظرفیت و تقاضا نشان دهیم:

    \begin{flalign*} \text{Maximize} & \: \sum_{t=1}^{\bar{t}} rS_{t}-hI_{t}&\\ \text{Subject to:} & \: S_t\leq d_t\hspace{1cm} t=1,...,\bar{t}&\\ & X_t\leq c_t \hspace{1cm}t=1,...,\bar{t}&\\ & I_{t}=I_{t-1}+X_{t}-S_{t}\hspace{1cm}t=1,...,\bar{t}&\\ & X_{t},S_{t},I_{t}\geq 0 \hspace{1cm}t=1,...,\bar{t} \end{flalign*}

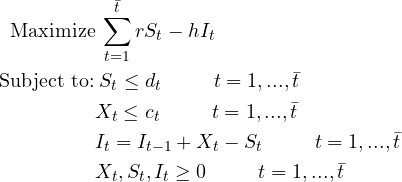
تابع هدف، حداکثر سود را با ضرب سود هر واحد r در فروش هر دوره St و کم کردن هزینه نگهداری موجودی باقیمانده h در پایان دوره t و برای تمام دوره‌ها در افق برنامه‌ریزی محاسبه می‌کند. محدودیت اول نشان می دهد که فروش نمی توند از مقدار تقاضا بیشتر باشد.

 دوم اینکه نمی توانیم بیشتر از ظرفیت کارخانه تولید کنیم. محدودیت سوم مربوط به تعادل موجودی است و می گوید موجودی پایان دوره t برابر است با موجودی باقیمانده از دوره قبل بعلاوه محصولی که این دوره تولید کردیم اما فروش نرفته است (Xt-St). در آخرین محدودیت نیز نشان می دهیم که متغیرهای تصمیم نمی توانند اعداد منفی باشند.

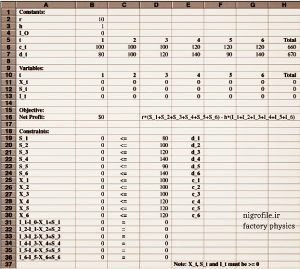
اکنون یک مثال ساده را در نظر می گیریم که به کمک اکسل آن را مدل و سپس حل می کنیم (شکل ۱). در این مثال سود هر واحد (r) 10 واحد پولی، هزینه نگهداری هر واحد کالا برای یک دوره (h) برابر یک واحد پولی، موجودی اولیه (I۰) نداریم و برابر صفر است و در نهایت افق برنامه ریزی برای ۶ ماه آینده است. سایر داده های مسئله در شکل مشخص است.

نحوه وارد کردن داده های مسئله در اکسل

شکل ۱- نحوه وارد کردن داده های مسئله در اکسل

    \begin{flalign*} \text{Maximize :} & \: 10(S_{1}+S_{2}+S_{3}+S_{4}+S_{5}+S_{6}) - 1(I_{1}+I_{2}+I_{3}+I_{4}+I_{5}+I_{6})&\\ \text{Subject to:} &\text{Demand constraints}&\\ & \: S_{1}\leq 80&\\ & \: S_{2}\leq 100&\\ & \: S_{3}\leq 120&\\ & \: S_{4}\leq 140&\\ & \: S_{5}\leq 90&\\ & \: S_{6}\leq 140&\\ &\text{Capacity constraints}&\\ & \: X_{1}\leq 100&\\ & \: X_{2}\leq 100&\\ & \: X_{3}\leq 100&\\ & \: X_{4}\leq 120&\\ & \: X_{5}\leq 120&\\ & \: X_{6}\leq 120&\\ &\text{Inventory balance constraints}&\\ & \: I_{1}-X_{1}+S_{1} = 0&\\ & \: I_{2}-I_{1} -X_{2}+S_{2} = 0&\\ & \: I_{3}-I_{2}- X_{3}+ S_{3} = 0&\\ & \: I_{4}-I_{3}- X_{4}+ S_{4} = 0&\\ & \: I_{5}-I_{4}- X_{5}+ S_{5} = 0&\\ & \: I_{6}-I_{5}- X_{6}+ S_{6} = 0&\\ &\text{Non-negativity constraints}&\\ & \: X_{1},X_{2},X_{3},X_{4},X_{5},X_{6}\geq 0&\\ & \: S_{1},S_{2},S_{3},S_{4},S_{5},S_{6}\geq 0&\\ & \: I_{1},I_{2},I_{3},I_{4},I_{5},I_{6}\geq 0&\\ \end{flalign*}

برای تمرین اطلاعات مسئله را مطابق شکل وارد اکسل نمایید. متغیرهای تصمیم که قبلاً معرفی شده اند را در گام اول برابر صفر قرار دهید و قرار است اکسل مقادیر بهینه برای آنها را پیدا کند. دقت کنید در قسمت محدودیت ها در قسمت B19 الی B30 اعدادش به این ترتیب وارد می شود که مثلاً سلول B19 را انتخاب کنید بعد مساوی را بنویسید و سلول B7 را انتخاب کنید. اگر خود عدد صفر داخل سلول B7 را داخل سلول B19  کپی کنید، اکسل نمی تواند جواب را پیدا کند.

 برای سلول B31 تا B36 باید یک فرمول ساده بنویسید. به عنوان نمونه برای سلول B31 می نویسیم B13 – B4 – B11 + B12 که معادل محدودیت (I۱ – I۰ – X۱ + S۱) می باشد. علامت کوچکتر یا مساوی مندرج در سلول های C19 الی C36، اعداد (D19:D36) و اندیس (E19:E30) برای خوانایی بهتر مدل نوشته شده و می توانید به صورت دستی وارد کنید.

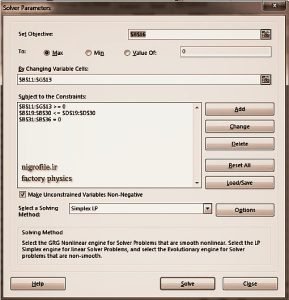
نکته بعدی برای وارد کردن اطلاعات مربوط به سلول B16 و تابع هدف است. فرمول این سلول به صورت  (B2*H12)-(B3*H13) نوشته می شود که معادل فرمول تابع هدف است. سلول های H12 حاصلجمع SUM(B11:G11) و سلول H13 نیز SUM(B13:G13) می باشد. اگر اطلاعات مسئله را درست وارد کردید در گام بعدی solver اکسل را فعال کنید. بعد وارد آن شوید باید پنجره ای شبیه تصویر (۲) را ببینید.

تنظیمات اکسل

شکل۲- تنظیمات اکسل

در قسمت بالا Max را انتخاب می کنیم. قسمت By changing (variable) cell باید محدوده سلول های متغیر تصمیم را انتخاب کنید و طبق تصویر وارد کنید. بعد نوبت وارد کردن محدودیت های مسئله است. دکمه Add را بزنید سلول ها و علامت محدودیت را انتخاب و OK را بزنید (شکل ۳).

اضافه کردن محدودیت ها

شکل۳- اضافه کردن محدودیت ها

در قسمت پایین پنجره اصلی مدل را Simlpex LP انتخاب کنید. در ادامه دکمه Option را بزنید و مقادیر  Max Time و Itertions را برابر ۱۰۰ قرار دهید. دیگه نکته ای نمانده و می توانید در پایین دکمه Solver را بزنید و نتیجه را مشاهده کنید. اینجا ممکن است با یکی از سه حالت زیر روبرو شوید:

۱- راه حلی پیدا نمی شود (Could not find a feasible solution)؛ احتمالاً این بدان معناست که مسئله غیرقابل اجرا است. یعنی هیچ راه حلی وجود ندارد که تمام محدودیت ها را برآورده کند. این ممکن است به دلیل یک خطای تایپی باشد (به عنوان مثال علامت مثبت به اشتباه به عنوان علامت منفی تایپ شده است) یا پاسخگویی به تقاضا با این ظرفیت ممکن نیست. در این مواقع یکبار دیگر فرمول بندی مسئله را مرور کنید تا مشکل پیدا شود.

 ۲- تابع هدف به یک عدد مشخصی همگرا نمی شود (Does not converge)؛ این بدان معنی است که یا الگوریتم نتوانسته است راه حل بهینه ای را در مدت زمان تعیین شده پیدا کند (برای همین زمان پردازش و تعداد تکرارها را در قسمت Option زیاد کردیم) یا اینکه الگوریتم به طور نامحدود راه حل بهتر پیدا می کند. این احتمال دوم زمانی رخ می دهد که مدل بدون کران (unbounded) باشد.

در همین مسئله اگر در اجازه دهیم که متغیرهای تصمیم بتوانند اعداد منفی نیز داشته باشند این اتفاق می افتد. یا در وارد کردن داده ها آنجا که تأکید داشتیم اعداد صفر اولیه (B11:G12) را در سلول های B19:B30 (شکل ۱) کپی نکنید به همین دلیل بود. (برای امتحان این کار را انجام دهید و نتیجه را ببینید).

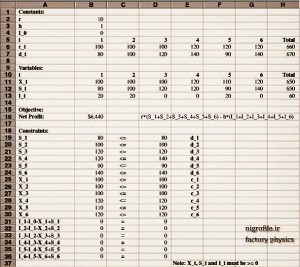
 ۳- پیدا کردن راه حل بهینه (Found a solution)؛ این نتیجه ای است که ما می خواهیم. در این حالت، برنامه مقادیر بهینه متغیرهای تصمیم، مقدار تابع هدف و محدودیت ها را در اکسل می نویسد. شکل (۴) نتیجه پیدا کردن راه حل بهینه برای مسئله را نشان می دهد.

خروجی نهایی اکسل

شکل۴- خروجی نهایی اکسل

قبل از تفسیر نتیجه بدست آمده ذکر این نکته ضروری است که اگر این مدل را با نرم افزار های تخصصی برنامه ریزی خطی حل کرده باشید یکی از امکانات این نرم افزارها ارائه تحلیل حساسیت است. اکسل هم این قابلیت را دارد ولی ممکن است در نسخه های کرک شده، فعال نباشد لذا تحلیل حساسیت را با توجه به همین نتیجه ارائه شده تشریح می کنیم.

با توجه به نتیجه بدست آمده اولین نکته ای که مشاهده می شود این است که مقادیر تولید با ظرفیت حداکثری موجود برابر نیست. در ماه ۵ باید ۱۱۰ واحد تولید کنیم در حالیکه ظرفیت موجود ۱۲۰ واحد است با توجه اینکه در ماه بعدی است تقاضا از ظرفیت تولید بیشتر است ممکن است کمی عجیب بنظر آید.

مقادیر بدست آمده برای برخی محدودیت ها دقیقاً برابر مقدار سمت راست آن شده که به آن مقید، الزام آور یا فعال (Binding or Tight) گفته می شود. برخی محدودیت ها نیز یکم قضیه رو شل تر گرفته اند (Nonbinding or Slack)  و غیر الزام آور هستند (S_4 و X_5 را ببینید).

به عبارت دیگر در ماه پنجم که باید ۱۱۰ واحد تولید کنیم در حالیکه ظرفیت ۱۲۰ واحد است اگر اینجا ظرفیت را ۱۱۹ واحد کنیم، جواب بهینه هیچ تغییری نمی کند. در مجموع می توانیم ۱۰ واحد از ظرفیت را کم کنیم (Slack) بدون تغییر در جواب بهینه. یا در ماه چهارم ۱۲۰ واحد می توانیم بفروشیم در حالیکه تقاضا در این ماه ۱۴۰ واحد است اینجا هم اگر تقاضا ۱۴۱ واحد بشود باز هیچ اتفاقی نمی افتد.

اما بر عکس در محدودیت های الزام آور تغییر در اعداد منجر به تغییر در جواب بهینه خواهد شد. برای مثال اولین محدودیت (X_1)  را در ماه اول در نظر بگیرد، ظرفیت تولید برابر ۱۰۰ واحد است و باید همین مقدار را تولید کنیم. حالا اگر یک واحد بیشتر تولید کنیم چه می شود؟

در ماه چهارم که تقاضا زیادتر از فروش است می توانیم این یک واحد اضافی را اینجا بفروشیم. هزینه نگهداری برای ۳ ماه معادل سه واحد پولی است اما قیمت فروش ۱۰ واحد پولی می باشد درنتیجه ۷ واحد پولی سود کسب خواهیم کرد (۷ واحد به تابع هدف اضافه می شود).

بر عکس اگر میزان تولید را در ماه اول بجای ۱۰۰ واحد ۹۹ واحد قرار دهیم در اینصورت در ماه سوم یک واحد محصول کم داریم. دقت کنید در ماه اول طبق نتیجه باید ۱۰۰ واحد تولید کنیم در حالیکه فروش ۸۰ واحد است و این ۲۰ واحد اضافه دقیقاً در ماه سوم مصرف می شود چرا که در این ماه میزان تقاضا ۱۲۰ و تولید ۱۰۰ واحد است.

حالا اگر قرار باشد در ماه اول ۹۹ واحد تولید کنیم اینجا ۲ واحد پولی هزینه نگهداری تا ماه سوم داریم و ۱۰ واحد پولی قیمت فروش که نتیجه می شود ۸ واحد پولی سود خالص که از دست می دهیم. معمولاً گزارشات تحلیل حساسیت سه نوع اطلاعات زیر را ارائه می دهد:

الف) قیمت سایه (shadow price)؛ نشان دهنده مقداری است که به ازای آن، تابع هدف با افزایش در مقادیر سمت راست محدودیت های الزام آور افزایش می یابد.

ب) افزایش مجاز (Allowable Increase)؛ نشان دهنده مقداری است که می توان به سمت راست اضافه کرد و قیمت سایه ای نیز کماکان معتبر باشد.

ج) کاهش مجاز (Allowable Decrease)؛ نشان دهنده کاهش در مقادیر سمت راست است با این شرط که قیمت سایه ای برای این محدودیت کماکان بکار رود.

در همین محدودیت اول (X_1)  که توضیح دادیم با افزایش یک واحد در تولید و فروش آن در ماه چهارم ۷ واحد پولی سود کسب می کنیم. این ۷ واحد همان قیمت سایه ای می باشد. در ماه چهارم معادل ۲۰ واحد کمبود محصول برای پاسخ به تقاضا داریم پس میزان افزایش مجاز در تولید ماه اول همین ۲۰ واحد است.

به مفهوم ساده تر تا ۲۰ واحد اگر در ماه اول اضافه تر تولید کنیم، هر واحد اضافه سودی معادل ۷ واحد پولی دارد. اما کاهش مجاز برای این محدودیت صفر است یعنی با کاهش تولید به ۹۹ واحد، قیمت سایه ای دیگر برای این محدودیت معتبر نیست.

اگر افزایش (کاهش) بیشتر از مقدار مجاز داشته باشیم باید یکبار دیگر مسئله را از اول حل کنیم. به طور خلاصه نتیجه ای که با این مثال ساده به دست می آید شامل:

۱-تغییر در اعداد سمت راست محدودیت های غیر الزام آور بر جواب بهینه تأثیر نمی گذارد. قیمت سایه یک محدودیت غیر الزام آور همیشه صفر است.

 ۲- افزایش عدد سمت راست یک محدودیت الزام آور، باعث افزایش جواب بهینه به میزانی برابر با (تعداد × قیمت سایه) می گردد، مشروط بر اینکه این افزایش کمتر یا مساوی حداکثر افزایش مجاز باشد.

 ۳- کاهش عدد سمت راست یک محدودیت الزام آور، جواب بهینه را به میزانی معادل (تعداد × قیمت سایه) کاهش می دهد، مشروط بر اینکه مقدار کاهش در دامنه مجاز باشد.

 ۴- تغییرات در اعداد سمت راست محدودیت های الزام آور کمتر یا بیشتر از حد مجاز، اثر نامشخصی بر جواب بهینه دارد و باید مدل یکبار دیگر حل شود.

 ۵- تحلیل حساسیت برای یک محدودیت الزام آور و در یک زمان اعمال می شود. اگر چندین تغییر ایجاد شود، تأثیر آنها لزوماً افزایشی نخواهد بود.

برنامه ریزی ادغامی در حالت چند محصولی (Product Mix Planning)

در ادامه، مثال قبلی را برای حالت چند محصولی توسعه می دهیم تا به شرایط واقعی نزدیک تر شود. یکی از موضوعات مهم در تولید چند محصولی بحث گلوگاه است. با توجه با اینکه تولید محصولات مختلف در ایستگاه های کاری نیاز به زمان های پردازش متفاوتی دارد در اینجا گلوگاه شناور خواهیم داشت و از برنامه ریزی ادغامی می توان برای شناسایی گلوگاه استفاده کرد. برای مدل سازی، از نمادهای زیر استفاده می کنیم:

i = اندیس محصول و i =1 . . .  ، m ، بنابراین m نشان دهنده تعداد کل محصولات است.

j = اندیس ایستگاه کاری، j =1 . . .  ، n ، بنابراین n تعداد کل ایستگاه های کاری را نشان می دهد.

t = اندیس دوره، t =1 . . .  ، ṫ ، بنابراین ṫ نشان دهنده افق برنامه ریزی است.

đit = حداکثر تقاضا برای محصول i در دوره t

 ḏit = حداقل فروش مجاز محصول i در دوره t

aij = زمان مورد نیاز در ایستگاه کاری j برای تولید یک واحد محصول i

cjt = ظرفیت ایستگاه کاری j در دوره t

ri = سود خالص از یک واحد محصول i

 hi = هزینه نگهداری یک واحد محصول i برای یک دوره t

Xit = مقدار محصول i تولید شده در دوره t

 Sit = مقدار محصول فروخته شده در دوره t

 Iit = موجودی محصول i در پایان دوره t (I۰  به عنوان اطلاعات اولیه از قبل مشخص است).

مثل مسئله قبل Xit ,Sit  و Iit متغیرهای تصمیم هستند در حالیکه باقی نمادها عدد ثابت بوده و جزء اطلاعات اولیه مسئله می باشند. برای حالت چند محصولی نیز مدل حداکثر سود را با توجه به محدودیت آن به شکل زیر تعریف می کنیم:

    \begin{flalign*} \text{Maximize} & \: \sum_{t=1}^{\bar{t}} \sum_{i=1}^{m} r_{i}S_{it}-h_{i}I_{it}&\\ \text{Subject to:} & \: \underbar d_{it}\leq S_{it} \leq\bar d_{it}\hspace{1cm} t=1,...,\bar{t}&\\ & \sum_{i=1}^{m}a_{ij}X_{it}\leq c_{jt} \hspace{1cm}t=1,...,\bar{t}&\\ & I_{it}=I_{it-1}+X_{it}-S_{it}\hspace{1cm}t=1,...,\bar{t}&\\ & X_{it},S_{it},I_{it}\geq 0 \hspace{1cm}t=1,...,\bar{t} \end{flalign*}

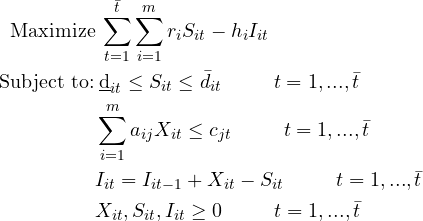
اولین تفاوت نسبت به مدل تک محصولی مربوط به محدودیت فروش است که اینجا نمی توان از یک مقدار کمتری بفروشیم (با توجه به در نظر گرفتن افق طولانی مدت). همچنین در محدودیت مربوط به ظرفیت، اینجا ظرفیت هر ایستگاه کاری را برای هر دوره در نظر می گیریم که همین امر به شناسایی ایستگاه کاری که محدودیت دارد کمک می کند. ایستگاه کاری که در چند دوره الزام آور باشد گلوگاه است.

اجازه دهید یک مثال از حالت چند محصولی را در نظر بگیریم که نشان می‌دهد چرا برنامه ریزی خطی به عنوان روش قدرتمندی شناخته می شود البته مفروضات ساده کننده ای در نظر گرفتیم که در دنیای واقعی خیلی ملموس نیست عنوان مثال تقاضا و ضرایب هزینه را از دوره ای به دوره دیگر ثابت فرض کردیم لذا دیگر دلیلی برای نگهداری موجودی نخواهیم داشت.

 به عبارت ساده تر اگر بتوانیم حداکثر تقاضای ماه جاری را با تولید فعلی برآورده کنیم با توجه به ثبات وضعیت، در دوره بعدی هم می توانیم همین کار را تکرار کنیم. تحت این شرایط به دنبال جواب بهینه در همین دوره فعلی هستیم. لذا دوره برنامه ریزی را برای یک ماه در نظر می گیریم.

حال وضعیتی را در نظر بگیرید که در آن یک شرکت دو محصول تولید می کند که ما آنها را محصولات ۱ و ۲ می نامیم. جدول (۱) اطلاعات مرتبط با تولید این دو محصول را نشان می دهد. هزینه مواد خام در جدول درج شده است، برای نیروی کار و سایر هزینه های ثابت سرجمع مبلغ ۵۰۰۰ واحد پولی در نظر می گیریم. علاوه بر این، ۲۴۰۰ دقیقه (۵ روز در هفته و یک شیفت ۸ ساعته) زمان در ایستگاه های کاری A تا D در دسترس است.

جدول۱- داده های اولیه مسئله چند محصولی برای یک دوره برنامه ریزی

محصول۱۲
قیمت فروش هر واحد۹۰ واحد پولی۱۰۰ واحد پولی
هزینه مواد خام۴۵ واحد پولی۴۰ واحد پولی
حداکثر فروش ماهانه۱۰۰۵۰
زمان تولید محصول در ایستگاه A (دقیقه)۱۵۱۰
زمان تولید محصول در ایستگاه B (دقیقه)۱۵۳۰
زمان تولید محصول در ایستگاه C (دقیقه)۱۵۵
زمان تولید محصول در ایستگاه D (دقیقه)۱۵۵

قبل از اینکه به مدلسازی مسئله فوق بپردازیم برای افزایش بینش و شهود خودمان ابتدا از دو روش دیگر برای حل این مسئله استفاده کرده بعد سراغ برنامه ریزی خطی می رویم.

الف) روش مبتنی بر هزینه (Cost Approach)

در ابتدا اجازه بدهید سراغ روش حسابداری هزینه برویم. هر واحد از محصول ۱ برابر ۴۵ واحد پولی (۴۵-۹۰) و محصول ۲ نیز ۶۰ واحد پولی (۴۰-۱۰۰) سودآوری دارند. در نتیجه منطقی است که از محصول ۲ بیشتر تولید کنیم. با توجه به اطلاعات جدول (۱) حداکثر فروش محصول ۲ برابر ۵۰ واحد است.

اگر بخواهیم همه این ۵۰ واحد را تولید کنیم باید به ظرفیت تولید نگاه کنیم و همانطور که میدانیم ظرفیت خط را گلوگاه تعیین می کند. بیشترین زمان پردازش محصول ۲ در ایستگاه کاری B با ۳۰ دقیقه می باشد بنابراین اول باید ببینیم این گلوگاه اجازه این مقدار تولید را می دهد یا نه.

۱۵۰۰ دقیقه = 50  واحد × ۳۰ دقیقه زمان پردازش به ازای هر واحد

کل زمان در دسترس ۲۴۰۰ دقیقه است و این یعنی تولید همه ۵۰ واحد امکانپذیر است. اما چقدر از محصول ۱ می توان تولید کرد؟ برای اینکار زمان باقیمانده را حساب می کنیم و دوباره گلوگاه را تشخیص می دهیم.

۱۹۰۰ دقیقه در ایستگاه کاری (A) = 2400 – 10(50)

۹۰۰ دقیقه در ایستگاه کاری (B) = 2400 – 30(50)

۲۱۵۰ دقیقه در ایستگاه کاری (C) = 2400 – 5(50)

۲۱۵۰ دقیقه در ایستگاه کاری (D) = 2400 – 5(50)

همانطور که ملاحظه می گردد مجدداً ایستگاه کاری B با کمترین زمان باقی مانده گلوگاه است. ظرفیت تولید محصول ۱ با توجه به اینکه تولید هر واحد از آن در همه ایستگاه های کاری از جمله گلوگاه ۱۵ دقیقه است را در نظر گرفته و کافیست ۹۰۰ دقیقه را بر ۱۵ تقسیم کنیم:

    \[\frac{900}{15} = 60\]

حداکثر ۶۰ واحد می توانیم از محصول ۱ تولید کنیم. سود کسب شده با این روش عبارت است از:

۷۰۰  = 5000- (۵۰×۶۰) +  (۴۵ ×۶۰)

آیا می توانیم بهتر عمل کنیم؟

ب) روش مبتنی بر گلوگاه (Bottleneck Approach)

اساس این روش بر این مفهوم است که بعد از شناسایی گلوگاه، سود کسب شده به ازای هر دقیقه پردازش محصولات تولیدی در گلوگاه را حساب کرده و محصولی که دارای بیشترین عایدی است در اولویت تولید قرار می گیرد. در این مثال، با در نظر گرفتن حداکثر میزان تولید محصول ۱ و ۲ محاسبات به ترتیب زیر خواهد بود:

۲۰۰۰ دقیقه در ایستگاه کاری (A) = 15(100) +10(50)

۳۰۰۰ دقیقه در ایستگاه کاری (B) = 15(100) + 35(50)

۱۷۵۰ دقیقه در ایستگاه کاری (C) = 15(100) + 5(50)

۱۷۵۰ دقیقه در ایستگاه کاری (D) = 15(100) + 5(50)

فقط ایستگاه کاری B به بیش از ۲۴۰۰ دقیقه (زمان در دسترس) نیاز دارد، بنابراین گلوگاه است. از این رو، می خواهیم بیشترین عایدی را از زمان در ایستگاه کاری B داشته باشیم. برای تعیین اینکه کدام یک از دو محصول این کار را انجام می دهد، نسبت سود خالص به دقیقه را در ایستگاه کاری B به صورت زیر محاسبه می کنیم:

    \[\frac{45}{15} = 3\]

    \[\frac{60}{30} = 2\]

این محاسبه، عکس نتیجه روش قبلی را نشان می دهد. با هر دقیقه پردازش محصول ۱ در ایستگاه کاری (B)، ۳ واحد پولی سود کسب می کنیم در مقابل ۲ واحد پولی برای محصول ۲. این محاسبه ساده می گوید که تولید محصول ۱ در اولویت بیشتری قرار گیرد. اگر ۱۰۰ واحد از محصول ۱ تولید کنیم (حداکثر مقدار) و از آنجایی که همه ایستگاه های کاری به ۱۵ دقیقه برای تولید هر واحد محصول نیاز دارند، زمان باقی در هر ایستگاه کاری برابر است با:

  ۹۰۰ دقیقه =۱۵(۱۰۰) – ۲۴۰۰

و از آنجایی که ایستگاه کاری B کندترین زمان عملیات برای تولید محصول ۲ را دارد، این ایستگاه گلوگاه بوده و ظرفیت تولید را مشخص می کند. هر واحد از محصول ۲ به ۳۰ دقیقه در ایستگاه B نیاز دارد. بنابراین، حداکثر مقدار تولیدی عبارت است از:

    \[\frac{900}{30} = 30\]

در نتیجه مبتنی بر این روش باید ۱۰۰ واحد محصول ۱ و ۳۰ واحد از محصول ۲ تولید کنیم که سود حاصل برابر است با:

۱۳۰۰ = 5000 – (۳۰ × ۶۰) + (۴۵ × ۱۰۰)

این به وضوح بهتر از ۷۰۰ واحد پولی است که با استفاده از تحلیل هزینه به دست آوردیم و به نظر می رسد بهترین کاری است که می توانیم انجام دهیم. اما آیا این روش همیشه جواب می دهد؟ در جواب باید گفت که در اغلب اوقات این روش به عنوان یک سلاح مخفی یا سلاح استراتژیک محسوب می شود.

 همانطور که در بخش های قبلی راجع به این روش صحبت شد، تأکید داشتیم که برخی از شرکت های تولیدی با تکیه به این روش توانسته اند میزان نقدینگی خود را بهبود دهند. اما بهرحال نمی توان گفت که همیشه بهترین جواب را می دهد.

 ج) روش برنامه ریزی خطی (Linear Programming Approach)

برای این منظور تغییر اندکی در داده های مسئله می دهیم و مشاهده خواهیم کرد که حتی این رویکرد قدرتمند هم در برخی مواقع نتیجه خوبی ندارد و بعد سراغ برنامه ریزی خطی می رویم. اصلاحات مد نظر شامل تغییر زمان پردازش محصول ۲ در ایستگاه B که از ۳۰ به ۳۵ دقیقه افزایش یافته است و در ایستگاه D نیز زمان پردازش برای محصول ۱ و ۲ از ۱۵ و ۵ دقیقه به ۲۵ و ۱۴ دقیقه تغییر یافته است (جدول ۲).

جدول۲- داده های اصلاح شده مسئله چند محصولی

محصول۱۲
قیمت فروش هر واحد۹۰ واحد پولی۱۰۰ واحد پولی
هزینه مواد خام۴۵ واحد پولی۴۰ واحد پولی
حداکثر فروش ماهانه۱۰۰۵۰
زمان تولید محصول در ایستگاه A (دقیقه)۱۵۱۰
زمان تولید محصول در ایستگاه B (دقیقه)۱۵۳۵
زمان تولید محصول در ایستگاه C (دقیقه)۱۵۵
زمان تولید محصول در ایستگاه D (دقیقه)۲۵۱۴

در ادامه با توجه به تغییرات انجام شده ابتدا گلوگاه تولید را با توجه به حداکثر تولید شناسایی می کنیم.

۲۰۰۰ دقیقه در ایستگاه کاری (A) = 15(100) +10(50)

۳۲۵۰ دقیقه در ایستگاه کاری (B) = 15(100) + 35(50)

۱۷۵۰ دقیقه در ایستگاه کاری (C) = 15(100) + 5(50)

۳۲۰۰ دقیقه در ایستگاه کاری (D) = 25(100) + 14(50)

 ایستگاه کاری B همچنان گلوگاه است، اما اکنون ایستگاه کاری D نیز از ۲۴۰۰ دقیقه موجود فراتر رفته است. اگر ایستگاه کاری B را به عنوان گلوگاه تعیین کنیم، نسبت سود به زمان پردازش محصول در گلوگاه برابر است با:

    \[\frac{45}{15} = 3\]

    \[\frac{60}{35} = 1.71\]

نتیجه مانند قبل نشان می دهد که باید تا حد امکان از محصول ۱ تولید کنیم. اما با دقت در داده های جدول ۲ مشاهده می گردد که این ایستگاه کاری D است که برای محصول ۱ گلوگاه است. حداکثر مقداری که می توان در ایستگاه D و در مدت زمان ۲۴۰۰ دقیقه تولید کرد برابر خواهد بود:

    \[\frac{2400}{25} = 96\]

از آنجایی که ۹۶ واحد از محصول ۱ از کل زمان در دسترس استفاده می کند، ما نمی توانیم هیچ محصول ۲ را تولید کنیم. بنابراین سود خالص حاصل از این ترکیب عبارت است از:

۶۸۰ –  = 5000 –  (۹۶ × ۴۵)

نتیجه حاصل جالب است و با این محاسبات ما ضرر خواهیم کرد. شاید به این دلیل که ما از ایستگاه B در محاسبات استفاده کردیم در حالیکه این ایستگاهD  بود که محدودیت در تولید محصول ۱ ایجاد می کرد. دوباره از اول محاسبات را با ایستگاه D انجام می دهیم:

    \[\frac{45}{25} = 1.80\]

    \[\frac{60}{14} = 4.29\]

اینبار نشان می دهد که تولید محصول ۲ سودآورتر است. از آنجایی که ایستگاه کاری B برای محصول ۲ کندترین ایستگاه است، بررسی می کنیم تا ببینیم چه مقدار محصول ۲ می توانیم تولید کنیم بنابراین :

    \[\frac{2400}{35} = 68.57\]

از آنجایی که این مقدار از حداکثر تقاضا (جدول ۲ را ببینید) بیشتر است، باید حداکثر مقدار محصول ۲ که همان ۵۰ واحد است را تولید کنیم. اینجا زمان باقی مانده خواهیم داشت که برای تولید محصول ۱ استفاده می شود. اما چقدر زمان باقی مانده داریم؟ با محاسبات زیر داریم:

۱۹۰۰ دقیقه در ایستگاه کاری (A) = 2400 – 10(50)

۶۵۰ دقیقه در ایستگاه کاری (B) = 2400 – 35(50)

۲۱۵۰ دقیقه در ایستگاه کاری (C) = 2400 – 5(50)

۱۷۰۰ دقیقه در ایستگاه کاری (D) = 2400 – 14(50)

با تقسیم زمان باقی مانده بر دقیقه های لازم برای تولید یک واحد محصول ۱ در هر ایستگاه، حداکثر تولید محصول ۱ را در هر ایستگاه به ما می دهد:

    \[\frac{1900}{15} = 126.67\]

    \[\frac{650}{15} = 43.33\]

    \[\frac{2150}{15} = 143.33\]

    \[\frac{1700}{25} = 68\]

توجه داشته باشید که ایستگاه B کمترین زمان در دسترس را دارد و تولید محصول ۱ را با محدودیت مواجه می کند و در نتیجه میزان نهایی تولید همان ۴۳ واحد است. سود نهایی عبارت است از:

۶۵- واحد پولی = 5000 – (۵۰ × ۶۰) + ( ۴۳× ۴۵)

و ما همچنان در حال ضرر کردن هستیم. لذا در گام آخر مسئله فوق را به کمک برنامه ریزی خطی مدل و حل می کنیم. X۱ و X۲ به ترتیب مقدار تولید محصول ۱ و ۲ می باشد.

    \begin{flalign*} \text{Maximize :} & \: 45X_{1}+60X_{2} - 5000&\\ \text{Subject to:} & \: X_{1}\leq 100&\\ & \: X_{2}\leq 50&\\ & \: 15X_{1} + 10X_{2}\leq 2400&\\ & \: 15X_{1} + 35X_{2}\leq 2400&\\ & \: 15X_{1} + 5X_{2}\leq 2400&\\ & \: 25X_{1} + 14X_{2}\leq 2400&\\ & \: X_{1},X_{2}\geq 0&\\ \end{flalign*}

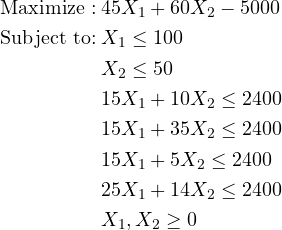
با حل این مسئله در اکسل جواب زیر به دست می آید:

  ۵۵۷/۹۴ = جواب بهینه

X∗۱ = 75/۷۹

X∗۲ = 36/۰۹

البته اگر این اعداد را گرد کنیم جواب بهینه برابر خواهد بود با:

۵۳۵  = 5000 – (۳۶ ×۶۰) + (۷۵× ۴۵)

بنابراین تولید هر چه بیشتر از محصول ۱ و یا محصول ۲ هر دو منجر به ضرر می شود. اما تولید ترکیبی از این دو محصول سود ایجاد می کند.  هر چند که می توان این مدل پایه را گسترش داد و مسائل پیچیده تری را مورد بررسی قرار داد اما یادتان باشد که هدف برنامه ریزی تولید ادغامی مربوط به آینده است و خیلی دنبال داده های دقیق و مدلسازی گسترده نباشید چرا که با گذشت زمان ممکن است شرایط تغییر کند (حس اصحاب کهف را بارها تجربه کردیم).

به طور خلاصه؛

الف) هیچ برنامه ریزی تولید ادغامی که بتواند برای هر موقعیتی جواب بهینه داشته باشد، وجود ندارد. یک برنامه ریزی ادغامی خوب، برنامه ای است که برای مسئله ی خاصی که شرکت با آن مواجه است طراحی شده است.

ب) سادگی مدل باعث افزایش درک آن می شود. اگرچه پرداختن به مسائل مختلف در برنامه ریزی تولید ادغامی مطلوب است، اما قابل درک نگه داشتن مدل از اهمیت بیشتری برخوردار است. با یک فرمول ساده شروع کنید. جزئیات بیشتر (به عنوان مثال محدودیت ها) را می توان بعداً اضافه کرد.

ج) برنامه نویسی خطی یک ابزار مفید برنامه ریزی تولید ادغامی است. افق برنامه ریزی طولانی مدت، نادیده گرفتن بسیاری از جزئیات تولید را توجیه می کند. بنابراین، محدودیت های ظرفیت، فروش و موجودی را می توان به عنوان محدودیت های خطی بیان کرد.

د) استحکام مدل (Robustness) مهم تر از دقت (precision) است. مهم نیست که داده ها چقدر دقیق و مدل چقدر پیچیده است، برنامه تولید شده توسط برنامه ریزی ادغامی هرگز دقیقاً دنبال نمی شود. عملیات تولید در واقعیت تحت تأثیر رویدادهای پیش بینی نشده ای قرار می گیرد که احتمالاً نمی تواند در برنامه ریزی ادغامی لحاظ شود.

ساده نگه داشتن مدل و در عین حال بررسی سناریوهای مختلف، می تواند بینش و شهود ما را از وضعیت های مختلف تولید که ممکن است در آینده با آن مواجه شویم افزایش دهد.

گوبلای خان

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

error: Content is protected !!